This page lists all synthetic option strategies (follow the links for more details and examples of individual strategies). It also explains how synthetic positions relate to the positions which they are imitating, mainly in terms of position value, cash flow, and payoff at expiration.
The List
- Long Call Synthetic Straddle
- Long Call Synthetic Strangle
- Long Combo
- Long Put Synthetic Straddle
- Long Put Synthetic Strangle
- Short Call Synthetic Straddle
- Short Call Synthetic Strangle
- Short Combo
- Short Put Synthetic Straddle
- Short Put Synthetic Strangle
- Synthetic Call – see Synthetic Long Call
- Synthetic Covered Call
- Synthetic Covered Put
- Synthetic Covered Strangle
- Synthetic Long – see Synthetic Long Stock
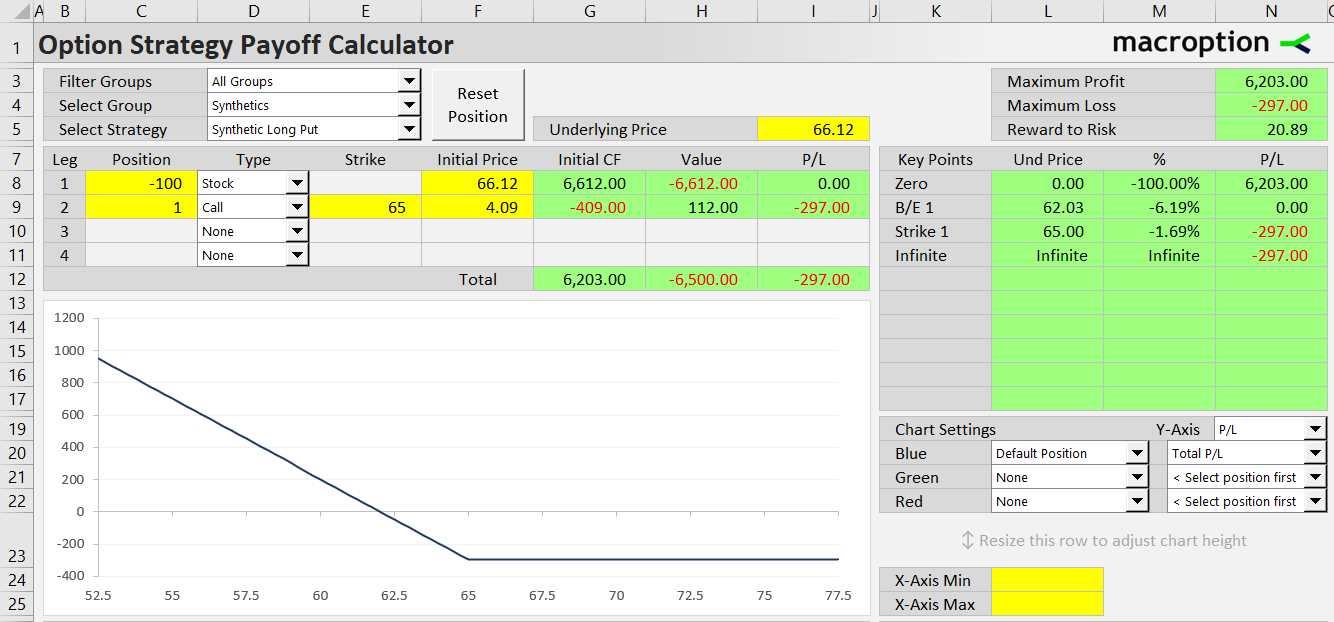
- Synthetic Long Call
- Synthetic Long Put
- Synthetic Long Stock
- Synthetic Put – see Synthetic Long Put
- Synthetic Short – see Synthetic Short Stock
- Synthetic Short Call
- Synthetic Short Put
- Synthetic Short Stock
- Synthetic Stock – see Synthetic Long Stock
- Synthetic Straddle – see Long Call Synthetic Straddle
- Synthetic Strangle – see Long Call Synthetic Strangle
What Synthetic Strategies Do
Synthetic option strategies imitate the payoff and risk exposures of other strategies using different securities.
For example, a combination of short underlying and long call option creates the same payoff as a long put option (with the same strike as the call) – this strategy is known as synthetic put.
Put-Call Parity
The reason why synthetic positions work and reliably create the desired exposures is the close relationship between the prices of calls, puts, and the underlying asset, known as put-call parity:
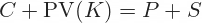
... where:
- C = Call option price
- P = Put option price
- S = Underlying price
- PV(K) = Ke-rT = Present value of strike price (same strike for call and put)
The above formula is behind virtually all the synthetic strategies.
Synthetic vs. Regular Position Value
Because a synthetic position has the same payoff as the position which it imitates, it would seem that their values should always be the same (otherwise an arbitrage opportunity would exist).
There is some truth to this logic, but in fact, the values don't always exactly match.
While having the same payoff at expiration as the original position, a synthetic position often has different cash flow.
Synthetic Position Cash Flow
For instance, a synthetic call option, created from long underlying and long put, requires a much higher amount of cash to set up (underlying price + put option premium) compared to plain long call option (call option premium only).
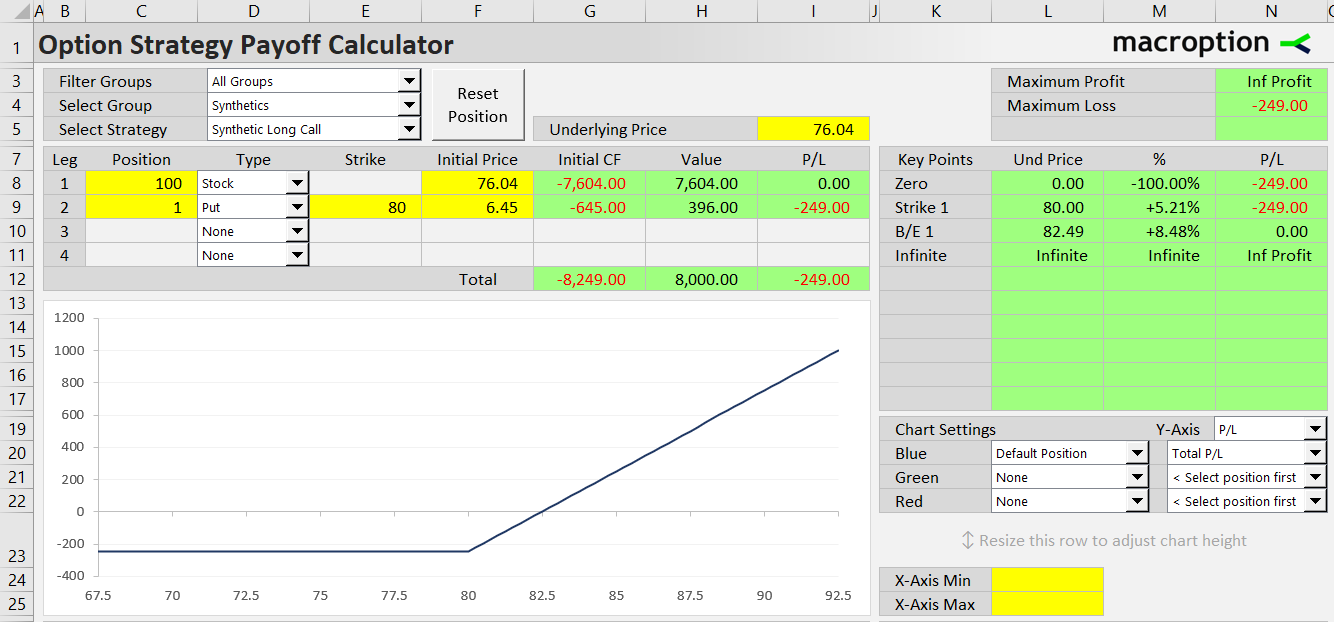
With time value of money and non-zero interest rates, two positions which have otherwise identical profit or loss but different cash flows must have different values, reflecting the interest (paid or received) on the cash amount that is different.
Quantifying the Value Difference
We can actually quantify the difference using the put-call parity formula:
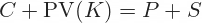
In this formula, P + S is the value of a synthetic call position, while C is the value of a call option with the same strike.
The formula shows that the difference between these two values equals PV(K) = present value of the strike. It depends not only on the strike itself, but also on the interest rate and time remaining to expiration.
As expiration approaches, PV(K) gets closer to K.
At expiration, the difference in values equals K, and profit or loss at expiration is identical regardless of underlying price.
Synthetic Strategies and Dividends
The above relationship with PV(K) gets more complicated with stock options.
If the underlying stock pays dividends during the life of the options, the holder of a synthetic call (stock+put) receives the dividend, while a call option holder does not. This must be reflected in their value difference.
The put-call parity formula with dividends is:

... adding PV(D), the present value of dividends, to the difference between the synthetic and regular position values.
Synthetic Strategies with American Options
The relationship is further complicated if the options are American (which stock options typically are) and there is the possibility of early exercise or assignment.
The put-call parity (in its equation form) only works for European options. With American options, the relationship between underlying, call, and put values is not fixed (due to the possibility of early exercise) and put-call parity becomes an inequality:
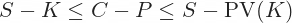
For American options with dividends it is:

There is still a close relationship between values of the synthetic position and the one it imitates, but it is no longer fixed with an equation.