Protective put, also called married put, is a simple option strategy designed to protect a long position in the underlying asset (such as a stock) with a put option.
Setup
A protective put position has two legs:
- Long underlying
- Long put option
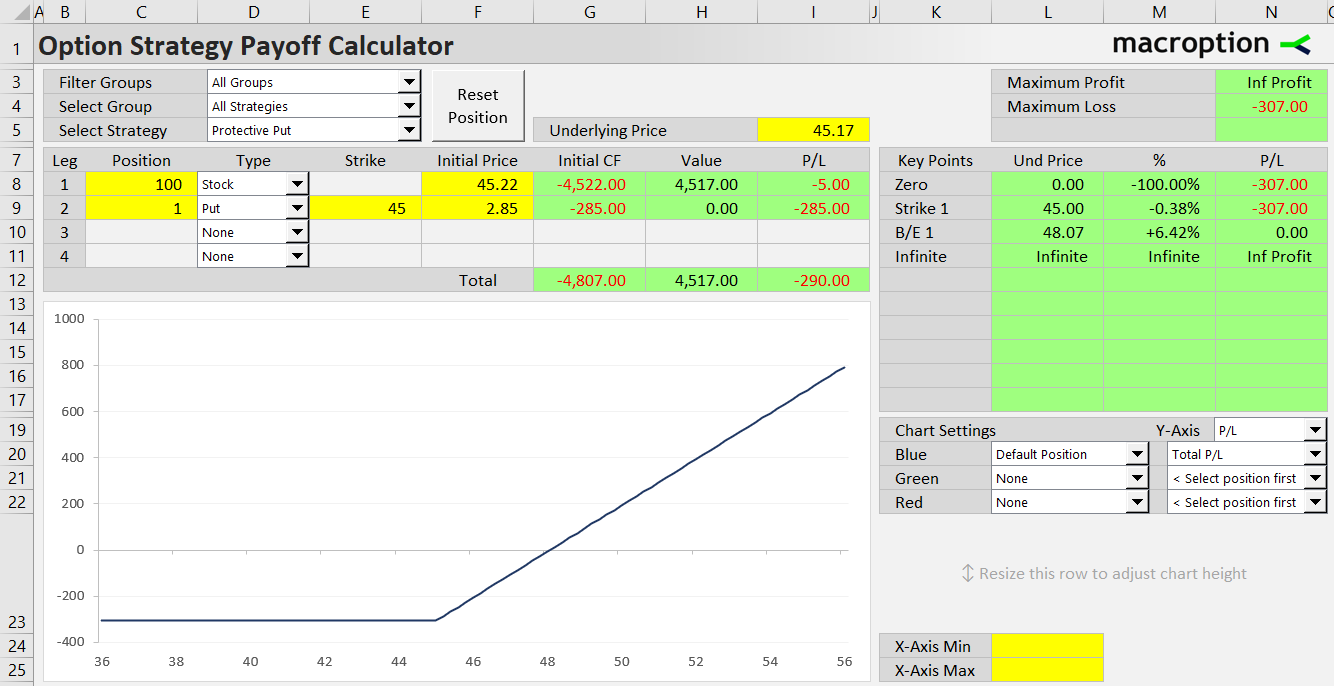
Payoff at Expiration
Protective put works like insurance (against losses in the underlying position): When buying insurance (the put option), you need to pay premium (the put option price). The premium is non-refundable regardless of the eventual outcome – it reduces your total profit in exchange for the protection.
- If all goes well (underlying price goes up or at least does not fall), the put option expires out of the money.
- If underlying price falls below the put option's strike price, the put is in the money and its value helps offset losses from the long underlying position.
The exact payoff and P/L from a protective put position depends on the following:
- Initial underlying price (cost of buying the underlying position)
- Put option premium paid (cost of insurance)
- Put option strike price
- Underlying price at expiration
Total P/L is the sum of P/L from the underlying position (underlying price at expiration minus initial underlying price) and P/L from the put option (put option value at expiration minus premium paid).
P/L = P/L from underlying + P/L from put option
P/L = underlying price at expiration – initial underlying price + put value at expiration – put premium paid
Put value at expiration = MAX (strike – underlying price at expiration, 0)
Put option value at expiration depends on underlying price at expiration and put strike price:
- If the underlying price is at or above the strike, the put option expires worthless (its value at expiration is zero).
- If underlying price ends up below the strike, the put option is worth the difference (strike minus underlying price at expiration).
In the second case, you can either sell the put option just before expiration, collect the cash and keep holding the underlying, or exercise the put option and sell the underlying for the strike price (the financial outcome is the same; the only difference is whether you keep the underlying position or sell it).
Maximum Profit
Maximum possible profit from a protective put is infinite (assuming the underlying price can be infinitely high, which is true from stocks and most other underlying assets). It is just like a long position in the underlying, only reduced by the fixed amount of the put premium paid, which is usually quite small relative to the underlying price.
Maximum Loss
Maximum possible loss is limited – which is the very purpose of this strategy. If underlying price falls below the put strike, the put option gains value at the same rate as the underlying position loses value (assuming the same position size). Therefore, the P/L below the put strike is constant (as the formulas show below, the underlying price at expiration does not affect it).
Maximum loss = P/L at or below put strike = P/L from underlying + P/L from put option
P/L from underlying = underlying price at expiration – initial underlying price
P/L from put option = put strike – underlying price at expiration – put premium paid
Maximum loss = put strike – initial underlying price – put premium paid
Break-Even Point
The exact underlying price where total P/L turns from loss to profit and vice-versa is always above the put strike (below the strike P/L is constant). It is when profit from the underlying (underlying price at expiration minus initial underlying price) equals put premium paid. In other words, it is the underlying price that pays for the initial cost of both the underlying (initial underlying price) and the put option (put premium paid).
B/E = initial underlying price + put premium paid
If you have bought the underlying and the put option at different times and if the underlying increased before you bought the put, it is possible for the sum of initial underlying price and put premium paid to be lower than the put strike. In such case the position can't lose and there is no break-even point. Maximum loss is actually minimum profit.
When to Trade
Protective put is a suitable strategy when you hold a long position in the underlying asset and still expect underlying price to go up, but also want to protect the position against possible losses. Or you worry about a possible fall in underlying price in the near future, but don't want to close the long underlying position for some reason (e.g. expecting price increase in the long run, dividends, or tax reasons).
The cost and risk profile of a protective put position depends on strike and expiration of the put option.
Strike Selection
Put option premiums increase with increasing strikes, as higher strike puts are deeper in the money and lower strike puts are further out of the money. Therefore, the cost of protective put increases with put strike.
It is most common to select a strike that is at the money (strike close to current underlying price) or out of the money (lower strike) for protective put.
The lower strike you select, the cheaper the put option will be. This means lower initial cost (put premium paid) and higher profit if underlying price goes up (and you don't need the protection in the end). However, if underlying goes down, with lower strike the protection kicks in later. The put option only protects you against losses below the strike price.
The strike decision is mainly based on your risk tolerance (how big a loss you can accept in a worst-case scenario), how likely and how far you think the price can fall, and how much of your upside you are willing to sacrifice and spend on protection. If you are OK with higher risk and unwilling to spend too much on the put option, choose a lower strike (the extreme case – zero strike – is no protective put at all, just the plain and simple unprotected long underlying position).
Expiration Selection
You can think of put option expiration date as the duration of your insurance policy. The put only protects your underlying position until expiration – then you either need to buy another put option, or your underlying position becomes unprotected.
Options with more time to expiration are generally more expensive, but the relationship between time and option premium is not linear. It is cheaper to buy a 3-month option once than buy a 1-month option three times, if everything other than time remains unchanged.
In reality, factors like underlying price and volatility rarely remain unchanged for long. Therefore, although buying a longer dated put may be cheaper on paper, it may not be the best decision.
Let's say you have bought a 3-month protective put, but after the first month underlying price has increased by 20%. Now the put strike is quite far away from the new underlying price. The put is no longer a good protection. You may choose to adjust the position, sell the old low strike put and buy another put with strike closer to the new underlying price. But with the old put far out of the money now, you can't sell it for much. It would have been better to buy a 1-month put for lower premium in the beginning.
On the other hand, if underlying price doesn't move much during the first month, the original 3-month put doesn't need any adjustments and it is cheaper overall than a series of 1-month puts.
Liquidity is another factor to consider. Options with shorter time to expiration are generally more liquid than longer dated ones. On some underlyings, options as far as six or more months to expiration are still very liquid, on others their bid-ask spreads may be too wide, or the longer expirations may not be available at all.
Greeks
The put option does not need to be held until expiration. Perhaps the reasons why you seek protection no longer apply (you sell the underlying, or you no longer fear a price fall) and you may want to sell the put before it expires.
It is useful to understand how the put option price behaves as various factors (underlying price, volatility, time) change. This is measured by the Greeks.
Delta
Delta measures how the put option value changes when underlying price increases by $1.
Put options have negative delta, reaching values from -1 (deep in the money puts with strike well above underlying price) to 0 (far out of the money puts with strike well below underlying price).
The long underlying position also has delta – unlike the option is it constant at +1 (because the underlying asset's value increases $1 for every $1 increase in underlying price, obviously).
Because Greeks are additive, total protective put position delta is the sum of underlying delta (+1) and put delta (between -1 and 0). It can reach values between 0 (underlying price well below strike and put option deep in the money) and +1 (underlying price well above strike and put option far out of the money).
Notice how this corresponds to payoff at expiration discussed above: When underlying price is low, the put option neutralizes further losses in the underlying position – the combined position becomes immune to underlying price changes, which is expressed be delta close to zero. On the contrary, at high underlying price the put option has very little effect and the combined position behaves just like a long underlying position, with delta close to +1.
Gamma
Gamma measures the sensitivity of delta to changes in underlying price. Underlying position has zero gamma, as its delta is constant. Therefore, gamma of the entire protective put position depends only on the put option gamma (this is the case with all Greeks except delta).
The put option has positive gamma, though gamma itself changes with underlying price. It is highest (delta changes fastest) at the money, when underlying price is close to strike. As underlying price gets further away from the strike to either side, gamma approaches zero and delta becomes less sensitive. Simply said, most of the interesting action happens at the money, when underlying price is close to option strike.
Theta
Theta measures how the position's value changes with passing time, other things being constant. Underlying position has zero theta. Put option theta is negative (except some rare cases with European options) – the option loses value as time passes.
Vega
Vega measures sensitivity to changes in volatility. Underlying has zero vega. The put option has positive vega (greater volatility makes option premium higher). Like gamma and theta, the effect of volatility is most significant at the money and approaches zero as underlying price gets further away from strike.
Rho
Rho measures sensitivity to changes in interest rates. It is a bit more complicated, as it depends on underlying type. For put options on stocks, rho is negative (higher interest rates make put option prices lower). Protective put position on a stock has negative rho.
Protective Put vs. Long Call
You may have noticed that a protective put position behaves in many ways (payoff at expiration, Greeks) like a long call option position. This is not a coincidence (there is a close relationship between calls and puts with the same expiration and strike – see put-call parity).
That said, there are a few important differences between protective put and long call, especially with some types of underlyings (e.g. stocks):
- Cash flow: With protective put, you buy the underlying in the beginning, which means much higher initial cost.
- Rho: Calls have positive rho, puts (and protective put) negative.
- Dividends: With protective put, you own the underlying and receive dividends; with a call option you don't.