Tutorials and Reference
Expiration Calendars
Below you can find VIX futures and options expiration calendar for 2024, 2025 and 2026, as well as full VIX expiration dates history (2004-2023) and explanation of VIX expiration rules.
For standard US equity, index and ETF options (including options on VIX ETFs and ETNs) see:
Standard US Equity and
[more...]Below you can find options expiration calendar for 2024, 2025 and 2026 for standard US traded monthly and weekly equity, index, and ETF options, as well as expiration dates history for earlier years.
For VIX options and futures, see VIX Expiration Calendar.
Options Expiration Calendar 2024
Monthly option expirations:
19
[more...]Popular Pages
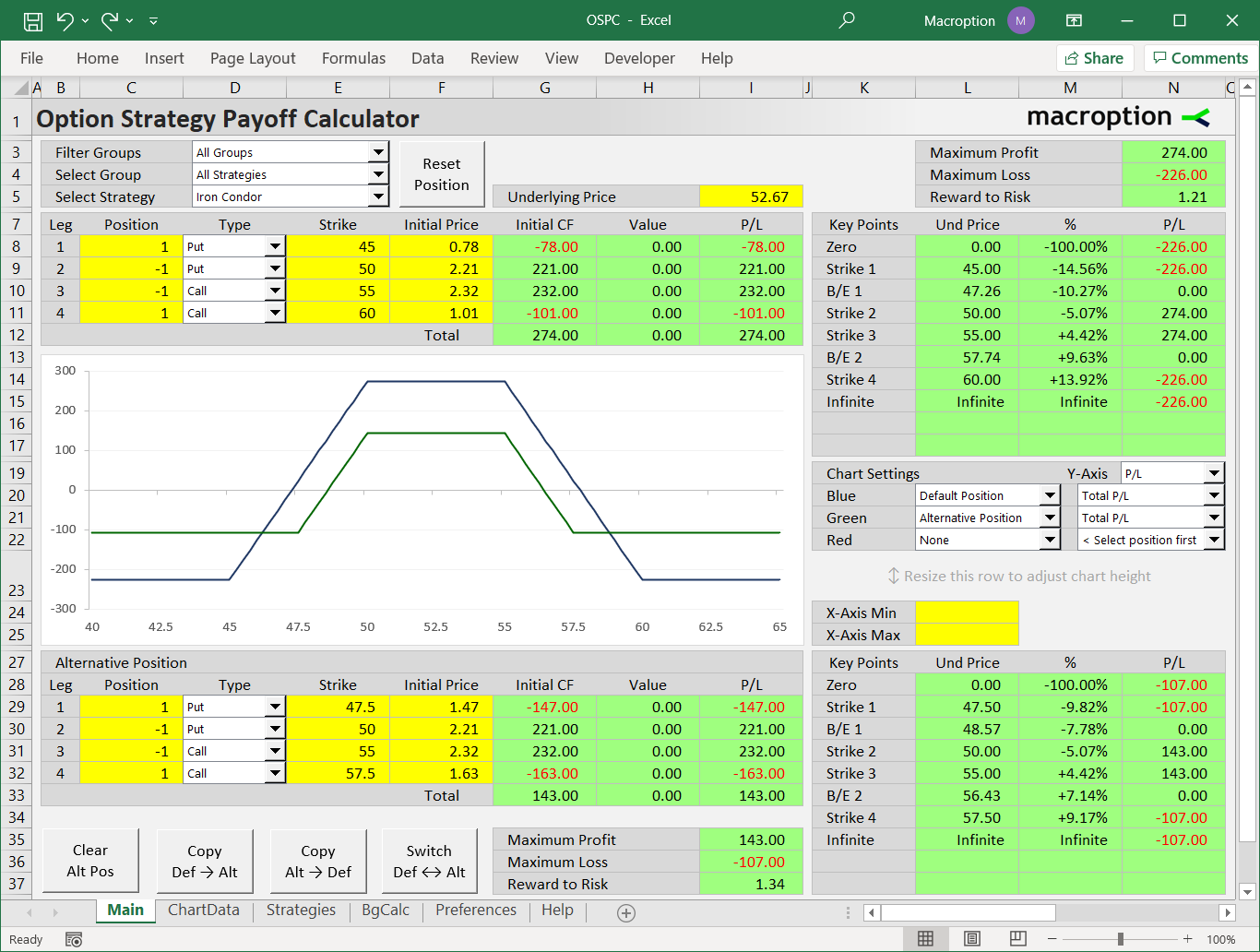
This is part 4 of the Option Payoff Excel Tutorial. In the previous parts (first, second, third) we have created a spreadsheet that calculates profit or loss for a single call or put option, given the strike price, initial option price and underlying price.
Now we are going to expand
[more...]This is part 5 of the Option Payoff Excel Tutorial, which will demonstrate how to draw an option strategy payoff diagram in Excel.
In the previous four parts we have explained option profit or loss calculations and created a spreadsheet that calculates aggregate P/L for option strategies involving up
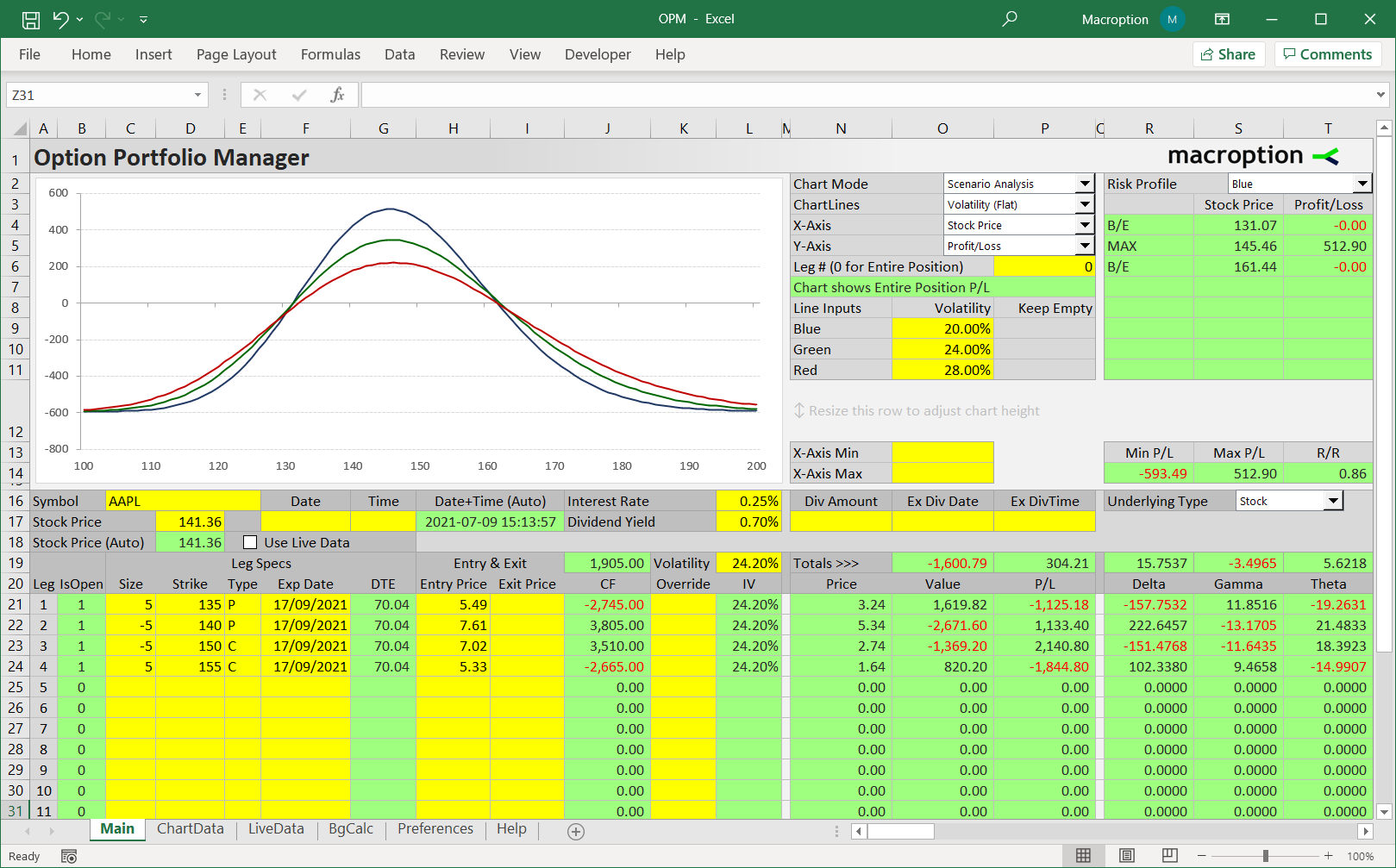
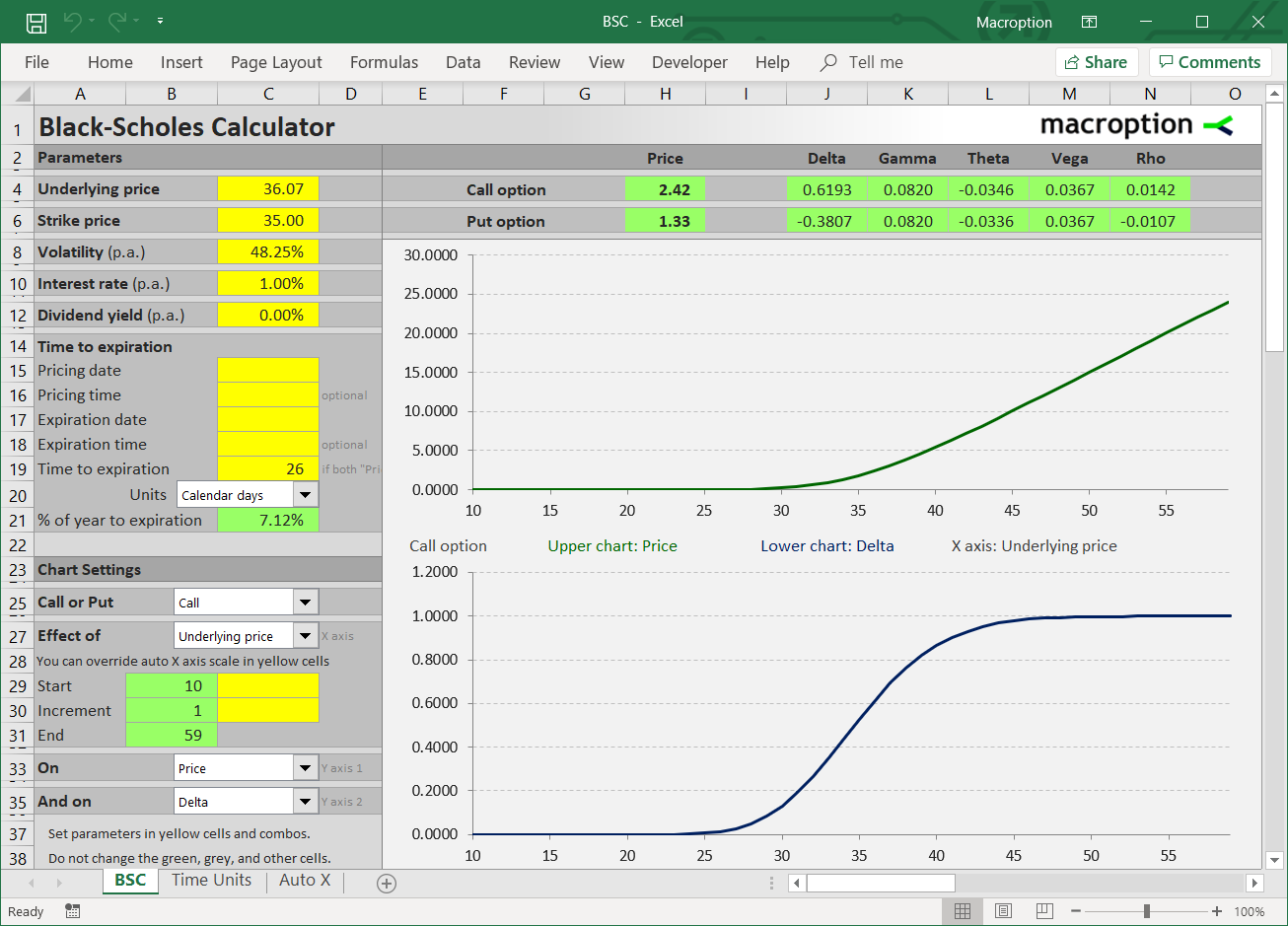
[more...]This page explains the Black-Scholes formulas for d1, d2, call option price, put option price, and formulas for the most common option Greeks (delta, gamma, theta, vega, and rho).
Black-Scholes Inputs
According to the Black-Scholes option pricing model (its Merton's extension that accounts for dividends), there are six parameters which
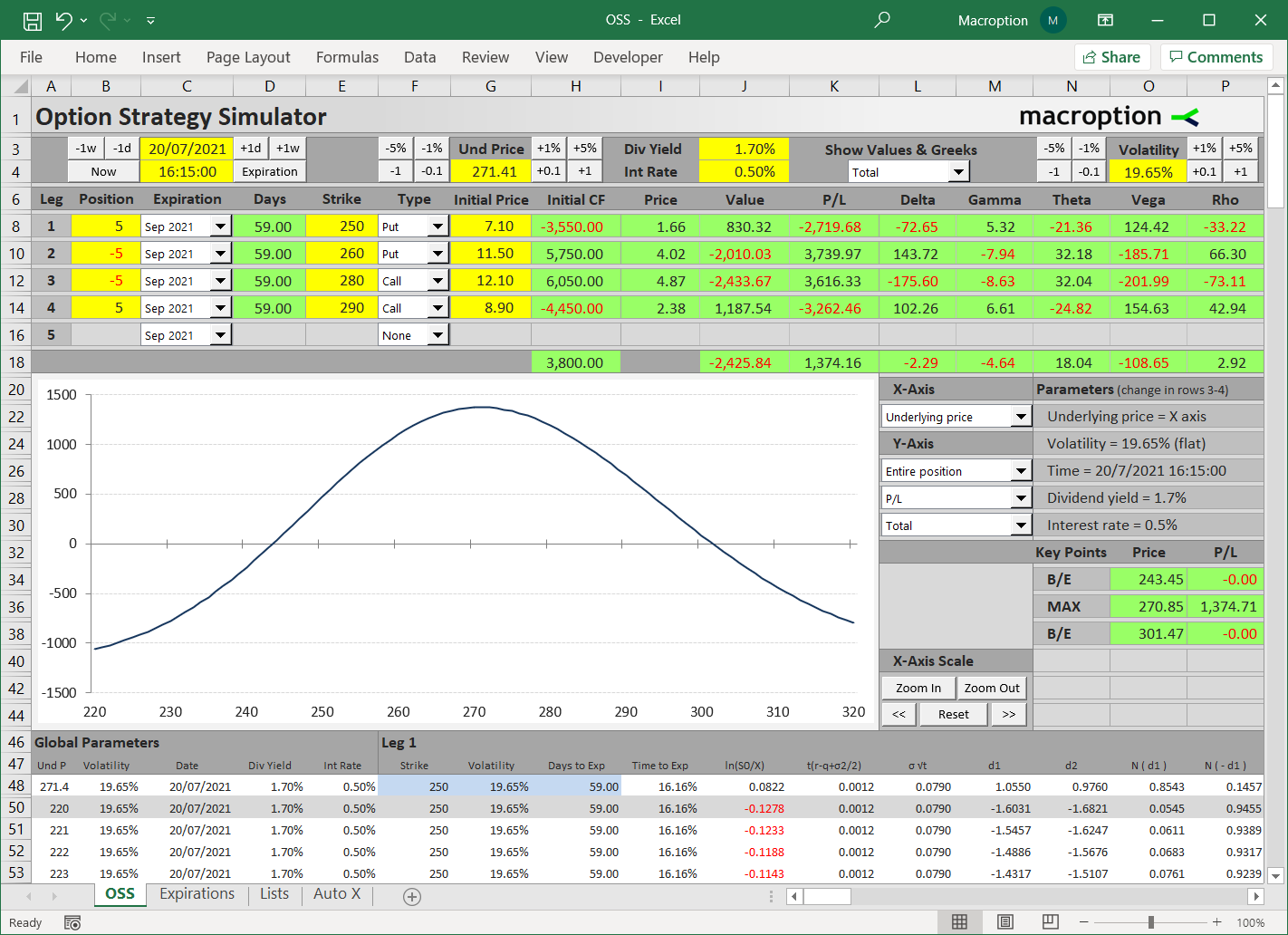
[more...]This page is a guide to creating your own option pricing Excel spreadsheet, in line with the Black-Scholes model (extended for dividends by Merton). Here you can get a ready-made Black-Scholes Excel calculator with charts and additional features such as parameter calculations and simulations.
Black-Scholes in Excel: The Big Picture
[more...]This is the second part of the Black-Scholes Excel guide covering Excel calculations of option Greeks (delta, gamma, theta, vega, and rho) under the Black-Scholes model.
Calculating Black-Scholes Greeks in Excel
I will continue in the example from the first part to demonstrate the exact Excel formulas. See the first
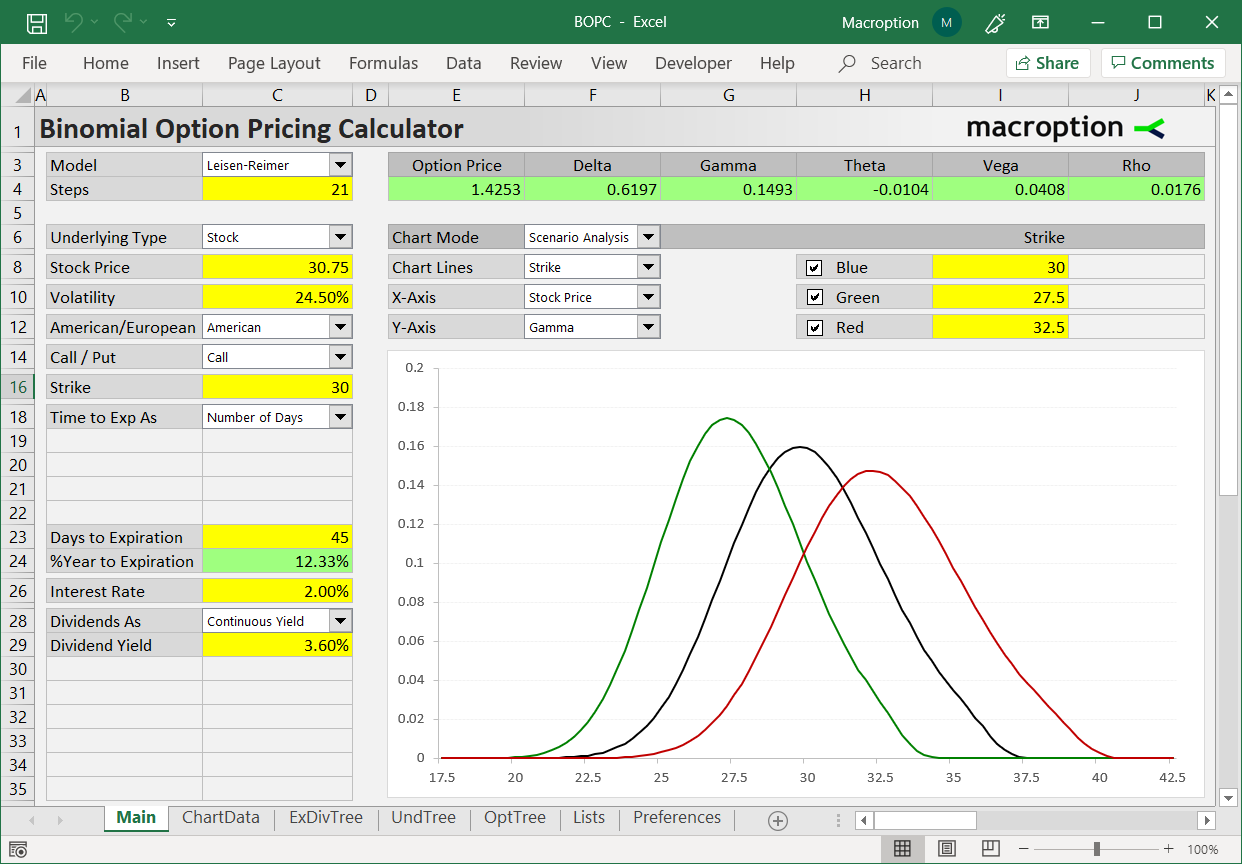
[more...]This page explains the logic of binomial option pricing models - how option price is calculated from the inputs using binomial trees, and how these trees are built.
Binomial Model Assumptions
All models simplify reality, in order to make calculations possible, because the real world (even a simple thing like stock
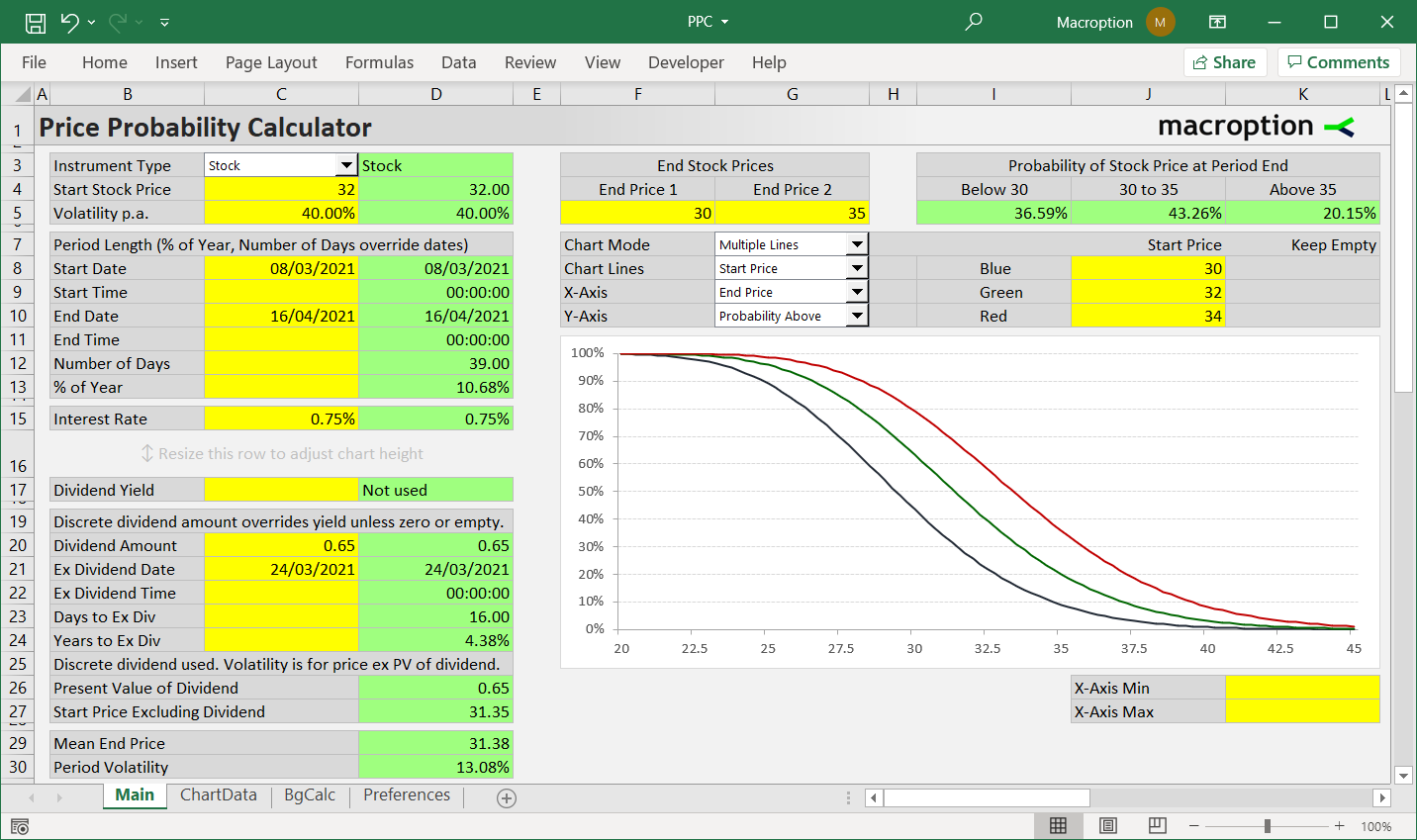
[more...]This page shows how to convert implied volatility (typically annual standard deviation of returns) to daily volatility and how to interpret it in terms of expected daily price changes with given probabilities.
Note that in the Implied Volatility Calculator you don't need to do the conversion, as the calculated implied
[more...]This page explains the logic of VIX calculation and some of the underlying assumptions and parameters. Exact formulas are available in VIX White Paper by CBOE.
If you are not familiar with the VIX index, you may first want to see a more basic explanation: What is VIX?
Basic Logic
[more...]VIX Futures Curve Explained
A futures curve is a curve made by connecting prices of futures contracts of the same underlying, but different expiration dates. It is displayed on a chart where the X-axis represents expiration dates of futures contracts and the Y-axis represents prices. The chart looks quite similar
[more...]This is detailed guide to calculating Average True Range (ATR) in Excel. We will first calculate true range and then ATR as moving average of true range. We will cover all three popular ATR calculation methods - simple, exponential, and the original Wilder's smoothing method.
You don't need advanced Excel skills
[more...]This page is a detailed guide how to calculate Relative Strength Index (RSI). You can see how the formulas work in Excel in the RSI Calculator. The calculation is explained in detail in chapter 4 of the calculator's guide.
RSI Formula
RSI = 100 - 100 / ( 1 + RS )
RS = Relative Strength = AvgU /
[more...]Put-call parity is a relationship between prices of European call and put options (with same strike, expiration, and underlying). It is defined as C + PV(K) = P + S, where C and P are option prices, S is underlying price, and PV(K) is present value of strike. This page explains
[more...]This page is an overview of main events and papers related to the Black-Scholes option pricing model. Besides works of its main authors, Black, Scholes, and Merton, we will also investigate earlier ideas which influenced the model, and other researchers (many of them famous for other models) who played a
[more...]