Put-call parity is a relationship between prices of European call and put options (with same strike, expiration, and underlying). It is defined as C + PV(K) = P + S, where C and P are option prices, S is underlying price, and PV(K) is present value of strike. This page explains the put-call parity formula, the no-arbitrage principle behind it, and its adjustments for dividends and for American options.
Put-Call Parity Formula Explained
Put-call parity is typically defined as:
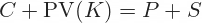
... sometimes also written as:
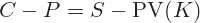
... where:
- C = Call option price
- P = Put option price
- S = Underlying price
- PV(K) = Ke-rT = Present value of strike price (same strike for call and put)
Put-call parity only holds for European options. Some sources use lowercase c, p for European options and uppercase C, P for American options, so the formula is:
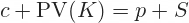
... or:

No-Arbitrage Principle
Like many other concepts in finance, put-call parity is based on the no-arbitrage principle:
If there are two assets or portfolios whose payoffs are the same under all future scenarios, they should have the same price.
If they don't, an arbitrage opportunity exists: You can make sure profit by buying the underpriced asset and simultaneously selling the overpriced asset.
Two Portfolios in Put-Call Parity
The two assets (or portfolios) in the put-call parity formula are:
- P + S = Put option and its underlying security.
- C + PV(K) = Call option and a (riskless government) bond or money market instrument.
When you hold a stock and a put option on it, it is effectively the same as holding a call option (with the same strike, expiration, and underlying) and bond with maturity same as the options and face value equal to the options' strike price.
Why are these two portfolios identical?
Three Scenarios at Expiration
At expiration, underlying price ST can be above, below, or equal to the options' strike K.
If ST > K:
- The put option expires worthless and the first portfolio is just the underlying. Its value is ST.
- The call option is in the money. You exercise it, which means you buy the underlying for the strike price K, which is exactly the cash you get from the maturing bond. You have the underlying, now worth ST. The two portfolios are identical.
If ST < K:
- The put option is in the money. You exercise it, which means you sell the underlying (which you have) for the strike price K. You are left with no securities, just cash amount K.
- The call expires worthless. The bond matures and you get its face value K. Same cash amount as the first portfolio.
If ST = K:
- The put expires worthless and the first portfolio is just the underlying – its value is ST. You can sell it in the market and get K in cash.
- The call expires worthless. The bond matures and you get its face value K. Same cash amount as the first portfolio.
Under all three scenarios, both portfolios end up with the same value when the options expire: The higher of ST and K.
If they always have identical outcomes in the future, the two portfolios should be worth the same now. If they are not, you can buy the underpriced one and sell the overpriced one, and make a sure profit.
This is why the put-call parity formula holds.
Put-Call Parity Formula with Dividends
If the underlying pays dividends, the logic of the no-arbitrage principle explained above still holds, with one small adjustment.
While a stock holder receives dividends, an option holder does not. Therefore, under all scenarios, the outcome of portfolio P + S will be greater than the outcome of portfolio C +PV(K), by a constant amount equal to present value of dividends PV(D).
The put-call parity formula with dividends is:

... where PV(D) is the present value of dividends paid during the life of the options.
Note that the discount factor used to calculate PV(D) is different from the discount factor used to calculate PV(K), unless the dividend is paid exactly at option expiration.
The put-call parity formula with the discount factors is:

... where t is the time from now until the dividend (assuming dividend ex-date and payment date are the same) and T is the time from now until the option expiration. Both are in years.
Put-Call Parity Formula for American Options
The no-arbitrage principle and the above equations do not apply for American options. The possibility of early exercise makes portfolio outcomes depend not only on underlying price at expiration ST, but also on the path it takes to get there.
That said, it is possible to identify upper and lower bounds for the difference between American call and put prices, using some of the no-arbitrage arguments.
The American put-call parity inequality is:
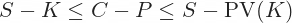
With dividends:
