This page provides examples how to price stock and ETF options in the Binomial Option Pricing Calculator.
Entering Inputs
To price stock or ETF options, select "Stock" in the Underlying Type dropdown box in cell C6.
Set the individual inputs in the cells below (C8-C26). Most of them work the same for all underlying types (see detailed instructions for each input). A specific feature of stock and ETF options is dividends – the calculator can work with either continuous dividend yield or discrete dividends. The examples below demonstrate how both types work. For more details see the dividends page.
Stock Option Example
Let's price a $40 strike call option on a stock which is currently trading at $41.04 (underlying price). The option expires in 71 days. It is quite a volatile stock; we expect its volatility over the life of the option to be 60% (annualized). The risk-free interest rate, which corresponds with the option's time to expiration, is 1.60%. The stock's dividend yield is 2.90%.
We will use the Leisen-Reimer model with 21 steps.
We need to set all the above inputs on the left side of the Main sheet (cells C3-C35). The correct inputs for this particular option are shown on the screenshot below.
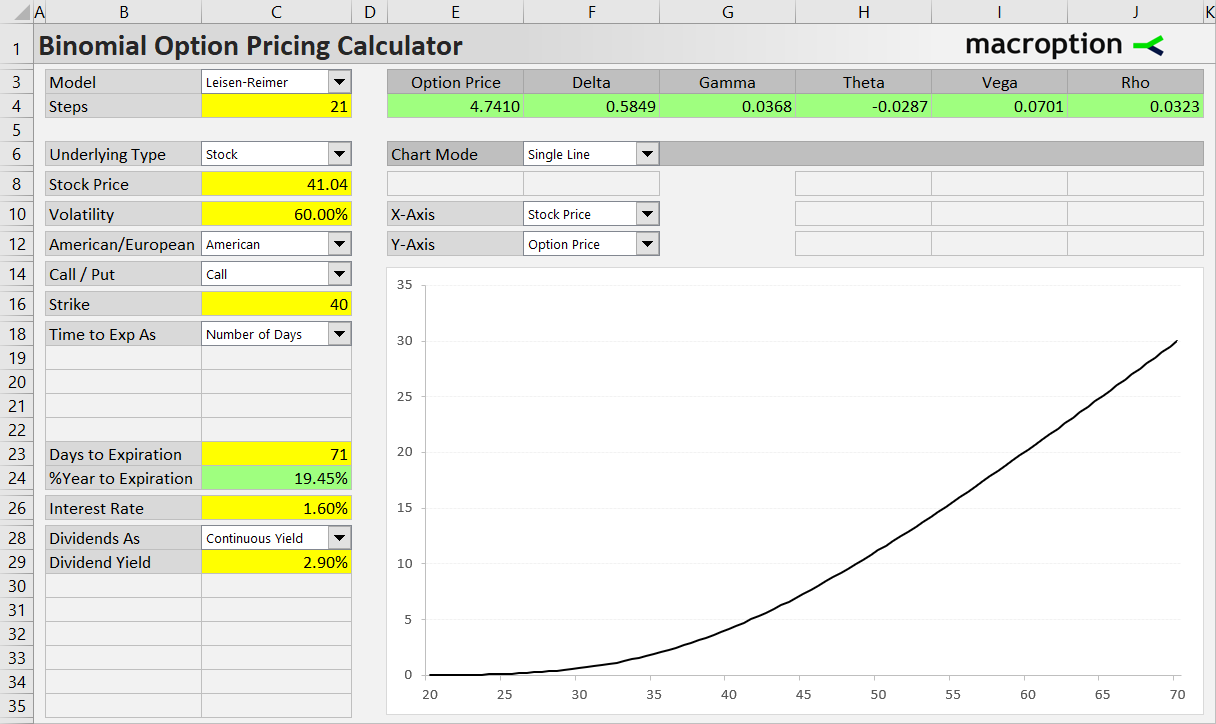
Once you corectly set all the inputs, you can see the resulting option price ($4.74 in this case) and Greeks in the green cells above the chart. In the chart you can model how individual inputs or their combinations affect the option price or Greeks.
Stock Option Example with Discrete Dividend
Now let's price another stock option, this time much closer to expiration – only 10 days. Current stock price is $34.85, the option's strike price is $35. This stock is less volatile than the former – we assume 26% volatility. It has much higher dividend yield at 8.03% and in only 3 days the stock will trade without the rights to the next quarterly dividend of $0.70 (time to ex dividend is 3 days and dividend amount is $0.70).
If we plug these inputs in the calculator with continuous dividend yield like in the former example, we get option price $0.50, which is in fact substantially overpriced. Using continuous dividend yield when the dividend is due very soon and its amount is high relative to the stock's price can lead to inaccurate results.
Stocks generally pay dividends in one or a few discrete amounts per year (quarterly in the US). Many models (in option pricing as well as other areas of finance) use continuous dividend yield, which is much simpler to work with, but it is a simplified model of reality. It is sufficiently accurate when the dividend payments are spread relatively evenly and/or their size is relatively small, but in cases like this, where the dividend is large and very soon, continuous yield can produce misleading results.
So let's price this option using discrete dividend amount by switching the dropdown box in cell C28 (Dividend As) to "Discrete Amount". The dividend yield input cell (C29) will hide and instead new input cells appear, allowing us to enter the dividend amount (0.70) in cell C30 and the number of days left to the ex dividend date (3) in cell C34.
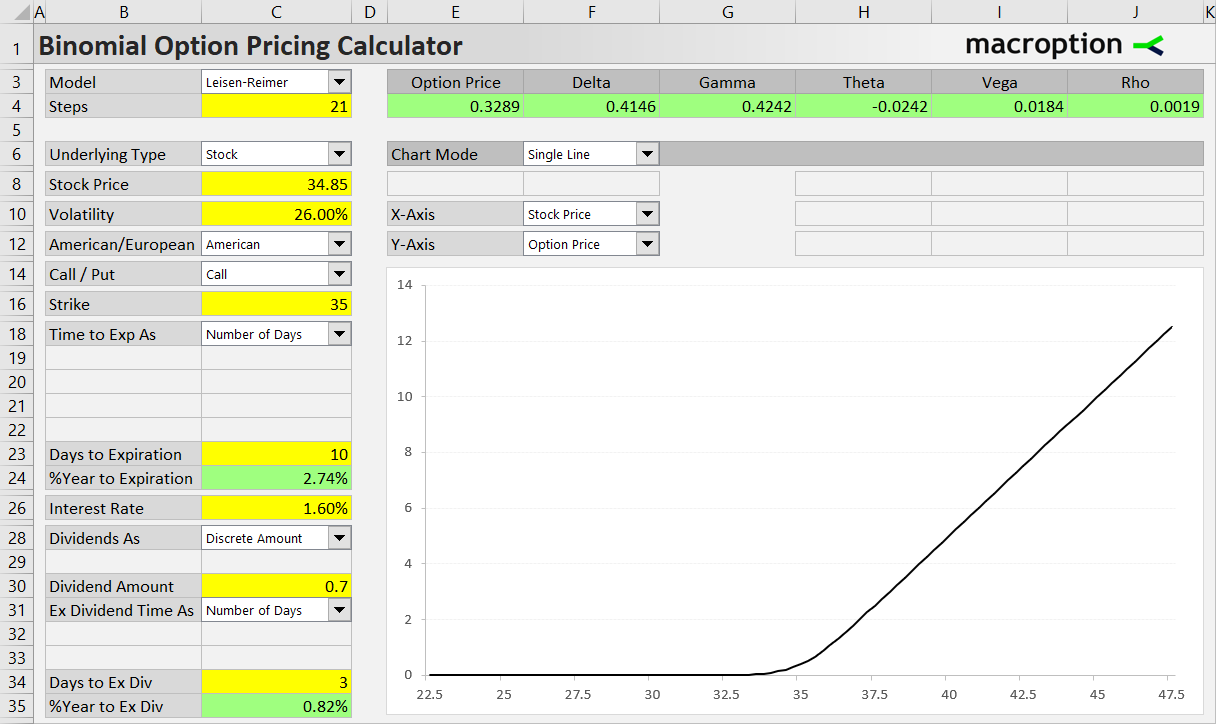
The resulting option price is now $0.33, which is much closer to reality.
It is safe to use continuous dividends with longer dated options or when the dividends are small relative to underlying price. For larger dividends coming very soon, it is more accurate to use the discrete dividend version of the pricing models.
ETF Option Example
For all purposes of option modeling and trading, ETFs work exactly the same as stocks. All the inputs are entered in the same way, and you can again use either continuous or discrete dividends. Therefore there is no separate selection for "ETF" in the underlying type dropdown box in cell C6 – just use "Stock".
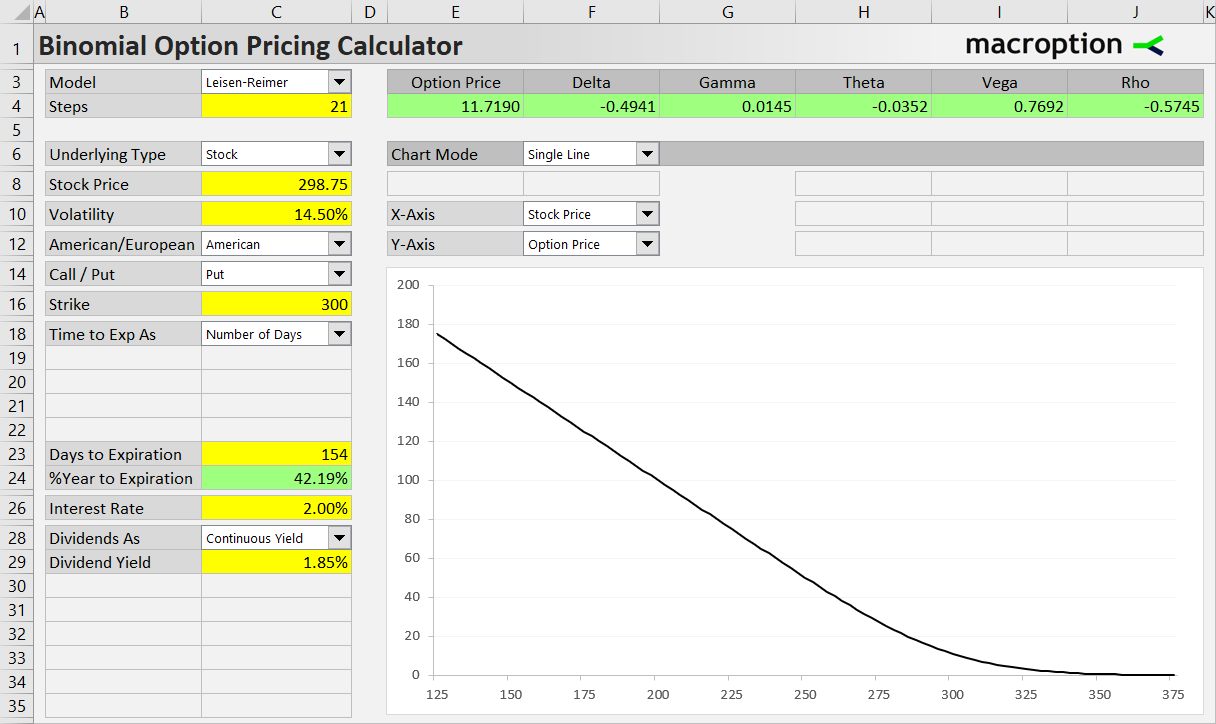
Let's price a $300 strike put option on a popular stock index ETF, which is currently trading at $299.35. The option expires in 154 days, we set volatility to 14.50%, dividend yield is 1.85% and interest rate 2.00%. All the inputs are shown below, as well as the resulting option price of $11.72.
Other Underlying Types
For instructions and examples of the other underlying types, see: