The page explains the OptTree sheet of the Binomial Option Pricing Calculator, where you can view the option price binomial tree.
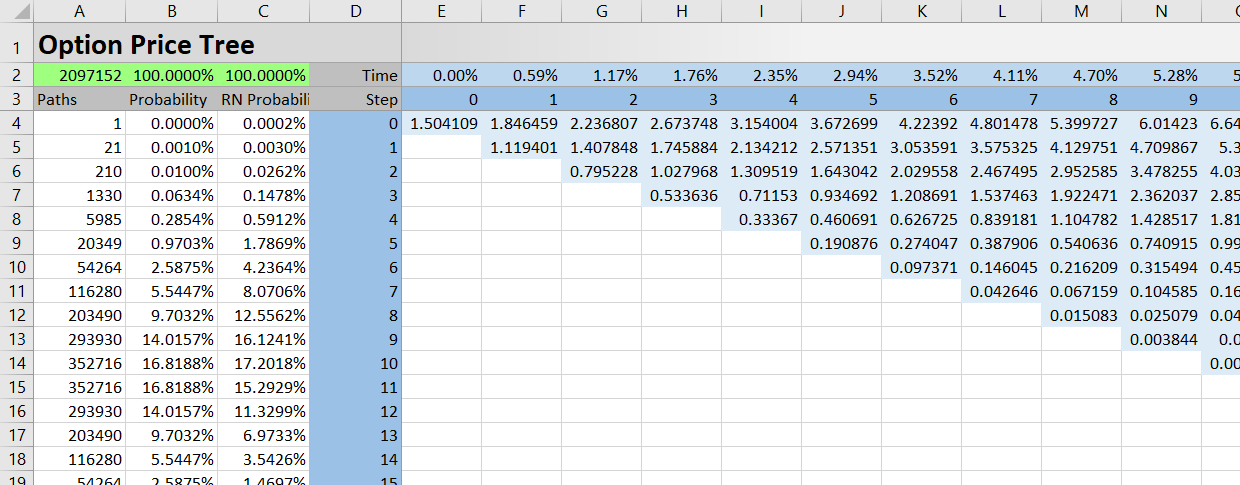
Option Price Tree Structure
The option price tree structure matches the underlying price tree structure in the UndTree sheet (see detailed explanation).
The tree itself is in column E (step 0) and beyond. Step numbers are in row 3. Time from valuation as percent of year is in row 2. Step 0 is the moment of valuation; the last step is option expiration. Number of nodes in each step equals the step number + 1, so each step has one node more than the step before.
How Option Prices Are Calculated
One difference between the underlying price tree and the option price tree is the direction of calculation. While the underlying price tree is calculated from left to right (from the current underlying price in step 0 to a range of underlying prices at expiration), the option price tree is calculated backwards – from option payoffs at expiration to current option price.
The Excel formulas in the OptTree sheet nodes (same formula in all nodes) may look complicated, but they are in fact just several simpler formulas combined in a nested IF function, because the calculations are different for 1) final node and earlier nodes 2) calls and puts.
Option Payoff at Expiration
Payoff at expiration in each final step node can be calculated from the final step underlying prices in the UndTree sheet. Because the tree sheets have identical layout, every cell in the OptTree sheet contains the same node as the cell in the same row and column in the UndTree sheet.
Calculating Earlier Nodes
Once we have payoff at expiration (the option's value) for all the final step nodes, we can go backwards through the binomial tree and calculate option prices at earlier steps. Every node's option price depends on option prices at the two nodes in the subsequent step (the node going up and the node going down). For American options, the model also checks at each node whether early exercise is profitable (this is when the option's intrinsic value is greater than the option's value calculated from the subsequent step nodes).
If both the subsequent nodes have zero option price, the current node's option price is also zero (generally option price is zero in every node from which all paths lead to the option expiring out of the money). For calls, usually some nodes in the bottom part of the tree (where underlying prices are low) will have zero option prices, while for puts it will be some nodes in the upper part (where underlying prices are high). How many and which exactly, depends on the particular combination of inputs.
Current Option Price
Once the option price calculations have gone backwards from the final step through the entire tree, the current (step 0) option price is calculated in cell E4.
Tree vs. VBA Calculations
The resulting option prices which you can see in the Main sheet and in the chart are not calculated in the tree sheets. Instead they use a custom VBA function named BinOp. The calculations are exactly the same, giving identical results. You can compare the option price values in cell E4 in OptTree (calculated from the tree sheets) and cell E4 in the Main sheet (calculated with the BinOp function).
Calculating binomial option prices in VBA rather than in Excel sheets has several advantages. Firstly, it doesn't require setting up separate tree sheets to calculate multiple option prices at the same time (such as for the chart). Secondly, it is faster. Thirdly, it makes calculation of the Greeks faster and easier.
In fact, the calculations in the Main sheet would work even if the tree sheets were removed from the calculator. The tree sheets are mainly for viewing prices at intermediate steps and nodes, which is not possible with the BinOp VBA function.