Entering Inputs

This page explains how to enter all the pricing inputs in the Binomial Option Pricing Calculator.

Required Inputs

To calculate option prices and Greeks with binomial models, you need the following inputs:

• Underlying security details: underlying type (e.g. a stock or currency), current underlying price, and, if applicable, whether the underlying security pays any dividends or yield
• Option details: whether it is a call or put, American or European, its strike price and time to expiration
• Risk-free interest rate

Where to Enter Inputs

Inputs are entered on the left side of the Main sheet, in cells B3-C35 (column C is the inputs themselves, column B is input labels).

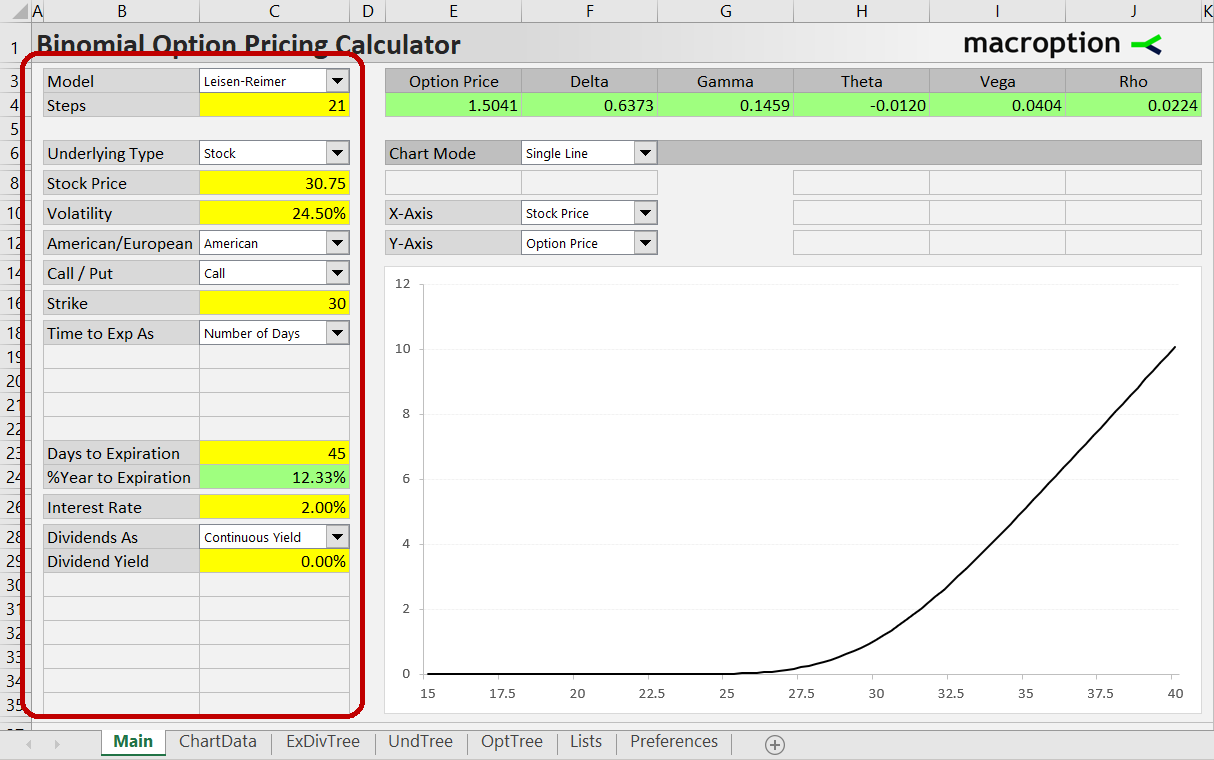
Set inputs by selecting from the dropdown boxes and by entering values in the yellow cells. Below you can find explanation of the individual inputs and cells.

Model and Number of Steps

Select the option pricing model in the dropdown box in cell C3.

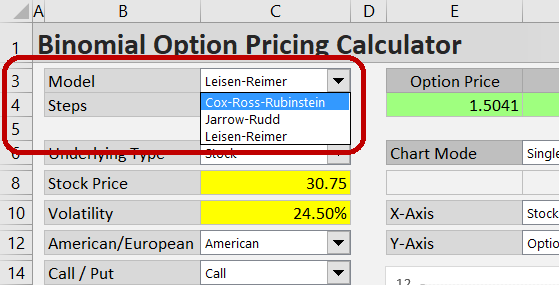
The calculator supports three different models:

• Cox-Ross-Rubinstein
• Jarrow-Rudd
• Leisen-Reimer

Enter number of steps in the yellow cell C4. Minimum is 2 (you need at least two steps to calculate option gamma). Maximum is 101 steps.

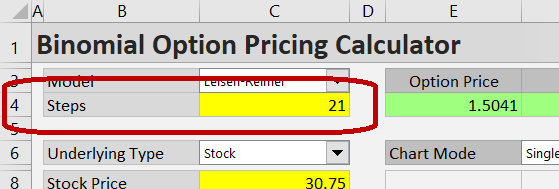
Binomial models are generally more accurate with higher number of steps, but more steps also require more calculations (number of nodes in binomial trees grows with steps squared). Therefore there is a tradeoff between accuracy and speed.

If you have no model preference, consider using the Leisen-Reimer model, which tends to become more precise faster (with fewer steps) compared to the other two – as few as 7 steps often gives option prices precise to 0.1% ($0.01 on a $10 option premium) or better.

Note that due to some specifics in the Leisen-Reimer model calculations, it may be less accurate with even number of steps, so make sure you always use odd steps with this model. The calculator is set to take care of this and automatically adjust the steps to the next higher odd number when you select even steps with Leisen-Reimer model (e.g. when you set 20 steps with LR model, it will use 21). You can switch off this autocorrection in the Preferences sheet, by setting the LRAdjustSteps option to FALSE.

When you first download the calculator, it is set to Leisen-Reimer model with 21 steps, which is more than sufficiently accurate for most purposes.

For more detailed discussion on models and number of steps, see the models section of this guide.

Underlying Type

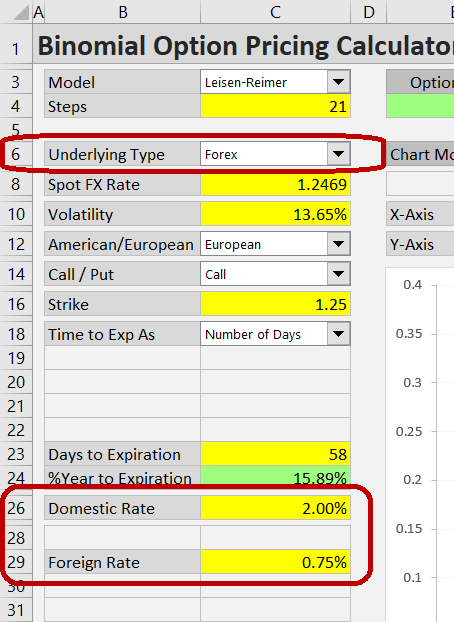
Select the type of underlying security in the dropdown box in cell C6.

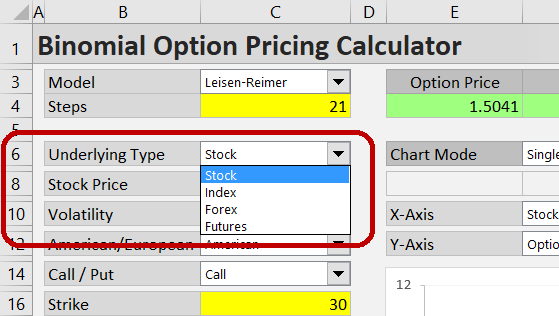
There are four underlying types to choose from:

• Stock – for options on stocks and ETFs
• Index – for index options
• Forex – for currency options
• Futures – for futures options

Main difference between them is how interest rates and dividends are treated by the pricing models.

When Stock is selected, the calculations will consider dividends, entered either as continuous dividend yield or as discrete dividend amount. Index options can also work with dividends, entered as continuous yield. You can find more details in the dividends section.

Currencies have no dividends, but currency option prices depend on two interest rates (of the two currencies in the FX pair). The pricing models use the second interest rate in place of dividend yield (because mathematically they are the same thing).

Futures options are different from all the other types due to the special relationship between underlying (futures) price and interest rate.

Underlying Price

Enter the current price of the underlying security in the yellow cell C8.

Its label (cell B8) will change depending on your underlying type selection.

For the Stock underlying type, the label will be "Stock Price". Enter the currenct stock price in cell C8.

For the Index type, the label will show "Index Value". Enter the current index value in cell C8.

For the Forex type, the label will be "Spot FX Rate". Enter the currenct spot rate. Make sure the direction is the same for both the spot rate and the option. For instance, if you are pricing an option on EUR denominated in USD, the spot FX rate to enter is EUR/USD (dollars per one euro, the way this pair is usually quoted). If it is an option on USD denominated in EUR, the spot rate must reflect that – enter number of euros per one dollar.

For the Futures type, the label will be "Futures Price". Make sure to enter the current futures price of the futures contract underlying the option, not the cash price of the underlying security to the futures contract.

Volatility

Enter volatility in the yellow cell C10. It should be in percent annualized, as volatility is usually quoted.

Volatility is one of the most difficult inputs to decide. Unlike underlying price, strike, or time to expiration, it is not fixed or easily observed in the market – it requires predicting the future (knowing the volatility of the underlying asset's price over the life of the option). It is where option pricing stops being exact mathematics and starts to involve experience and intuition.

There are various approaches to estimating volatility. You can use the underlying asset's historical volatility, the implied volatility of similar options (such as options on other stocks from the same industry), or a combination of these. It is also common to adjust volatility for seasonality and upcoming events (for instance, approaching company earnings tend to inflate implied volatility of stock options).

American/European

In the dropdown box in cell C12, select if the option is American or European.

These option types do not relate to the region where the options are traded, but to the way they can be exercised. American options can be exercised at any time until expiration, while European options can only be exercised at expiration. For instance, US traded stock options are American type, while most US traded index options are European type.

In many cases, the prices of American and European options with otherwise same specifications are the same. This is when the right to exercise the option prior to its expiration is worthless, which is true for most options most of the time, because by exercising early you give up the remaining time value. However, in some cases (e.g. some deep in the money puts or high dividend calls) an option's time value is actually negative and it makes sense to exercise early – therefore an American option will be worth more than an otherwise identical European option.

Unlike some other popular option pricing methods (like Black-Scholes), binomial models can correctly value the right to early exercise and are therefore accurate for both European and American options.

Call/Put

Select whether the option is call or put in the dropdown box in cell C14.

Strike Price

Enter the option's strike price in the yellow cell C16.

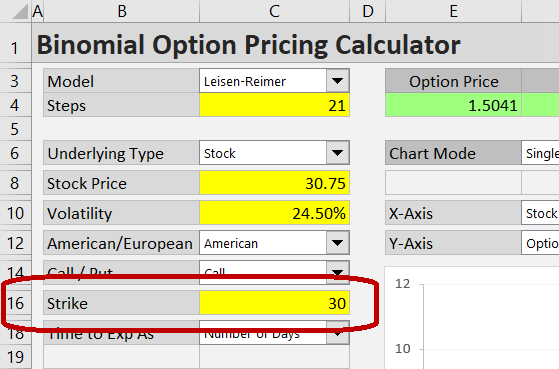
Make sure the units are the same in the underlying price (cell C8) and strike price (cell C16) inputs. With currency options, the direction of the FX pair must match (as has already been discussed in the underlying price input part).

Time to Expiration

For maximum flexibility, the calculator allows you to enter time to expiration in three different ways. This is selected in the dropdown box in cell C18.

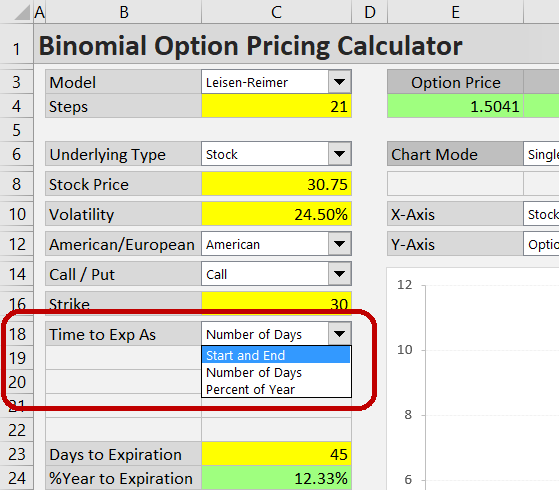
The options are:

• Start and End to enter valuation date (usually today's date) and expiration date (cells C19-C22)
• Number of Days to enter the number of days remaining to expiration (cell C23)
• Percent of Year to enter the percent of year remaining to expiration (cell C24)

Depending on your selection, the cells right below the dropdown box (C19-C24) will turn yellow, green or grey. Make sure to always overwrite yellow cells only. Green cells contain formulas and their values are calculated from what you have entered in the yellow cells. Grey cells are inactive and not currently used in the calculations.

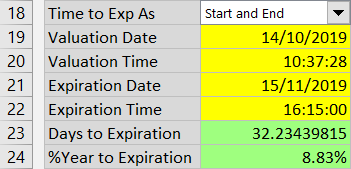
Entering Time to Expiration as Start and End

If you select "Start and End", you need to enter the valuation date in the yellow cell C19 and expiration date in cell C21. For greater precision, especially with short term options, you may also enter valuation and expiration time in cells C20 and C22, respectively. If you leave the time cells blank, effective time will be midnight (0:00). With Start and End format selected, number of days to expiration (cell C23, which is now green) is calculated as expiration date and time minus valuation date and time. Percent of year to expiration (green cell C24) is calculated as number of days divided by 365.

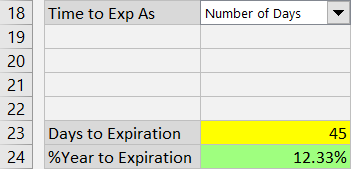
Entering Time to Expiration as Number of Days

If you select "Number of Days" in the dropdown box in C18, enter the number of days to expiration in the yellow cell C23. You can enter fractions of days, e.g. 12.25 for 12 days and 6 hours. The cells C19-C22 above (valuation and expiration date and time) will be grey, as these inputs are not needed now. Percent of year to expiration (cell C24) will be green and calculated from number of days entered in cell C23.

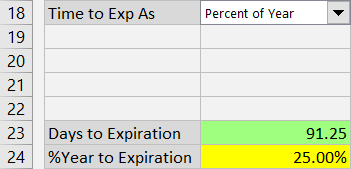
Entering Time to Expiration as Percent of Year

If you select "Percent of Year", enter the time to expiration as percent of year (number of days divided by 365) in the yellow cell C24. Cells C19-C22 are grey. Number of days in cell C23 (now green) is calculated from the entered percent of year in C24.

Interest Rate

Enter the risk-free interest rate in the yellow cell C26.

When pricing currency options, with Forex selected as underlying type, the label (in B26) will be "Domestic Rate". It should be the interest rate of the currency in which the option is denominated. For example, when pricing an option on EUR traded in USD, enter the USD risk-free rate in this cell. The "foreign", EUR interest rate in this example, will be entered in cell C29, whose label is "Foreign Rate" when Forex is selected as underlying type.

Dividends

Dividends only apply to stock, ETF and index options – when "Stock" or "Index" is selected in the underlying type dropdown box in cell C6.

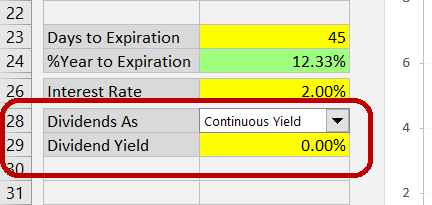
The calculator can work with dividends entered either as continuously compounded dividend yield or as a discrete dividend amount paid at a specific time. Choose the dividend format in the dropdown box in cell C28.

If you select Continuous Yield, enter the yield in the yellow cell C29.

If you select Discrete Amount, enter the dividend amount (per share) in the yellow cell C30. In the cells below, you also need to specify when this dividend will be paid.

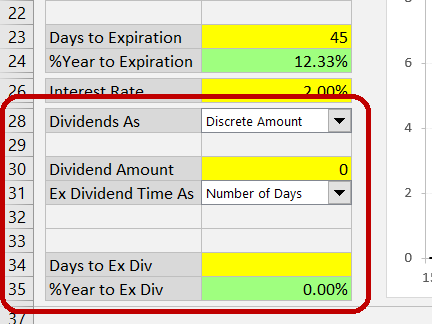
Like time to expiration, you can enter time remaining until the stock goes ex dividend in three different ways: as date (and optionally time), as number of days, or as percent of year (between valuation date and ex dividend date). Select the format in the dropdown box in cell C31. Depending on this selection, cells C32-C35 below will turn yellow, green or grey, following similar logic to the one described in the time to expiration section.

Note that discrete dividends will only affect the option price and Greeks calculations when the underlying goes ex dividend before the option expiration (time to ex dividend is smaller than time to expiration).

See more details about working with dividends and related features.

Option Price and Greeks

When all inputs are correctly set, you can see the calculated option price and Greeks in the green cells E4-J4.

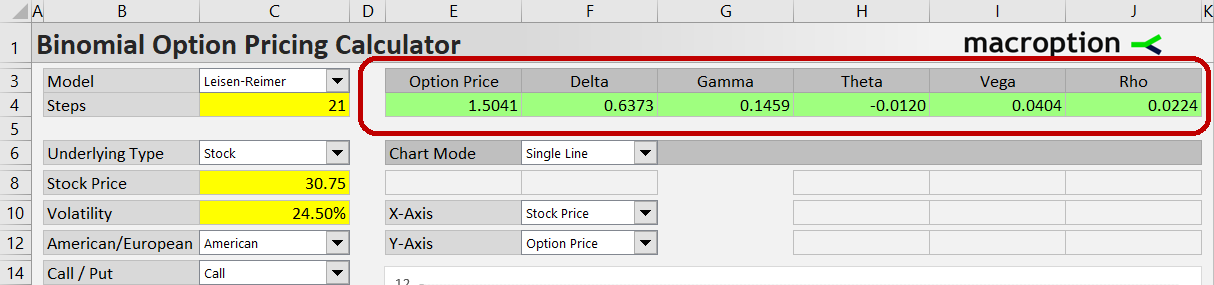
In other sheets (UndTree and OptTree), you can view the entire underlying price tree and the option price tree generated by the binomial model.

In the chart, which is located on the right side of the Main sheet, you can model various relationships between the inputs, option prices and Greeks. See how to work with the chart.