This page explains all settings in the Perefences sheet of the Binomial Option Pricing Calculator.
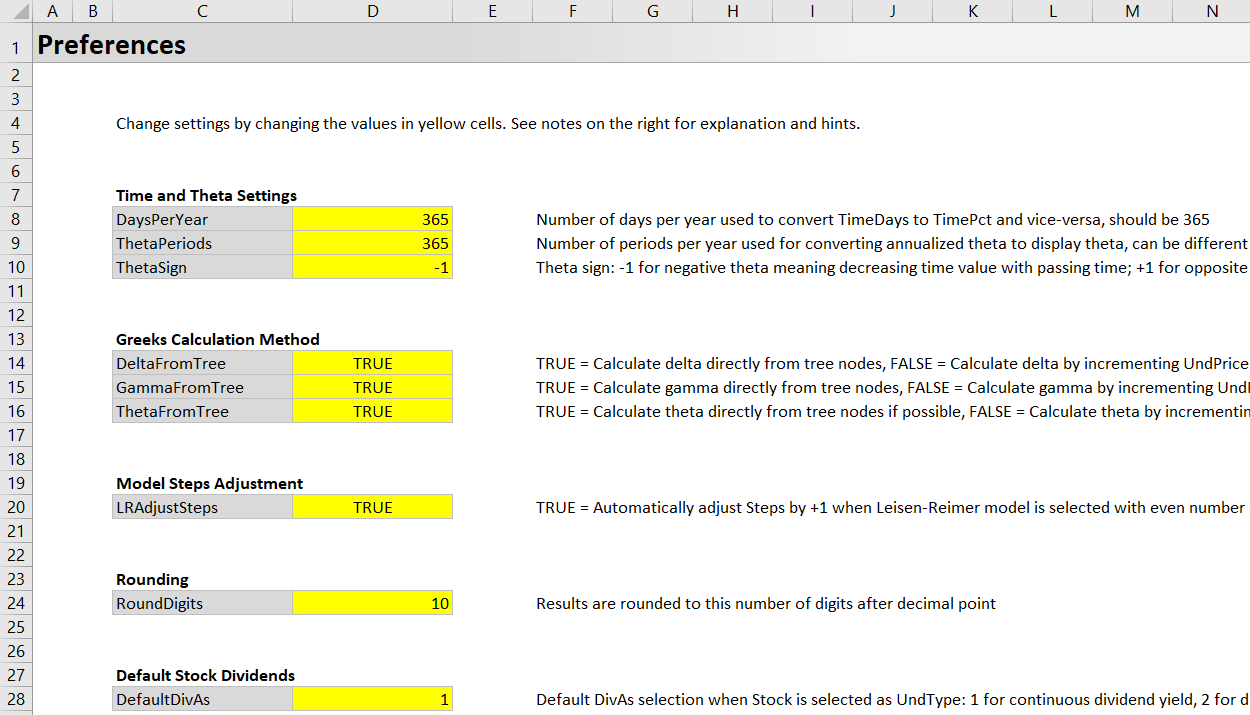
Time and Theta Settings
This section allows you to customize time computations and the units and sign of theta.
DaysPerYear (number, default 365) = Number of days per year, which is used for converting between different formats of time to expiration and time to ex dividend (days per year to percent of year and vice-versa).
ThetaPeriods (number, default 365) = Number of periods per year used for calculating theta. Option pricing models calculate theta annualized (how much the option price will change if time to expiration changes by one year), which is too long a period for most purposes. Therefore, the annual theta is divided by a certain number of periods per year to get theta for a shorter period, such as 365 (for theta per calendar day), 252 (for theta per trading day) or 52 (for weekly theta).
ThetaSign (-1 or +1, default -1) = If this setting is -1, theta will be displayed as negative number when the option loses value with passing time. If +1, positive.
Greeks Calculation Method
These settings control how individual Greeks are calculated. Each can be either TRUE or FALSE. When TRUE, the particular Greek is calculated directly from the binomial trees. When FALSE, it is calculated by incrementing the particular input. Both calculation methods are explained in the Greeks section of this user guide.
DeltaFromTree = TRUE to calculate delta from binomial trees.
GammaFromTree = TRUE to calculate gamma from binomial trees.
ThetaFromTree = TRUE to calculate theta from binomial trees for Cox-Ross-Rubinstein model. Other models calculate theta by incrementing time to expiration input regardless of this setting.
Model Steps Adjustment
LRAdjustSteps (TRUE or FALSE, default TRUE) = When TRUE, the calculator will automatically add one step when Leisen-Reimer model is selected with even number of steps (other models are not affected). For instance, when you enter 20 as number of steps (in the input cell C4 in the Main sheet) and have Leisen-Reimer selected as model, the calculator will actually generate binomial trees with 21 steps.
This is because Leisen-Reimer model can be inaccurate with even number steps, so odd steps are always recommended. If you want to use the calculator with Leisen-Reimer model and even steps for some reason, change this setting to FALSE.
Rounding
RoundDigits (integer, default 10) = Results, such as option prices and Greeks, and some intermediate calculations, such as binomial tree nodes, will be rounded to this number of digits after the decimal point. This is mainly to deal with floating point imprecision.
Default Stock Dividends
DefaultDivAs (1 or 2, default 1) = Unlike other underlying types, stocks can be modeled with continuous or discrete dividends in the calculator. This setting controls which format will be activated as default when underlying type selection (dropdown box in cell C6 in the Main sheet) is changed to Stock. 1 for continuous yield; 2 for discrete dividends. You can always change dividend format in the "Dividends As" dropdown box in cell C28 in the main sheet (it is only active when underlying type is Stock).
Chart Series Names
The final section at the bottom of the Preferences sheet allows you to customize the displayed names of the three chart series in Scenario Analysis. By default, the names are "Blue", "Green" and "Red"; you can change them to anything else by overwriting the text in the yellow cells next to Series1Name, Series2Name, Series3Name. For example, instead of "Blue", "Green", "Red", you can name the series "Default", "High", "Low".
These settings only affect the names (shown for example in cells H8, H10, H12 in the Main sheet), not the actual chart line colors. In other words, changing Series1Name to "Orange" will not make the chart line orange – you would have to change the actual chart settings the standard Excel way. The calculator's macros don't touch chart line colors in any way; they only display or hide entire lines.