This page explains the implementation of Cox-Ross-Rubinstein model in the Binomial Option Pricing Calculator.
All three models supported by the calculator – this one, Jarrow-Rudd and Leisen-Reimer – follow the same logic for constructing binomial trees (that part is explained in underlying price tree and option price tree).
The models only differ in sizes and probabilities of underlying price up and down moves in the underlying price tree. Cox-Ross-Rubinstein calculations of these are explained below.
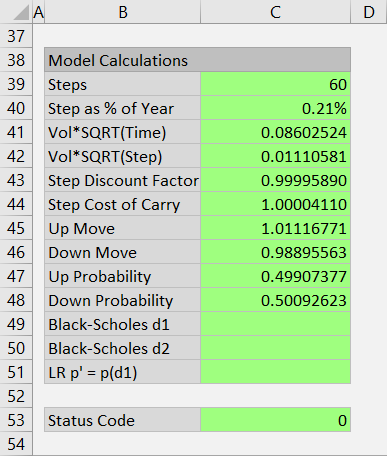
You can find these calculations in the Model Calculations section at the bottom of the Main sheet, in cells B38-C51.
Up and Down Move Sizes
In the Cox-Ross-Rubinstein model, up and down moves are symmetrical:
UpMove * DownMove = 1
... where UpMove and DownMove are single step price change multipliers expressed as 1 + %change, for example 1.25 for 25% up move and 0.80 for 20% down move.
In other words, when underlying price goes up one step and then down one step (or down one step and then up one step – order does not matter), it gets back to its original level.
As a result, the same prices repeat in subsequent steps of the CRR underlying price tree.
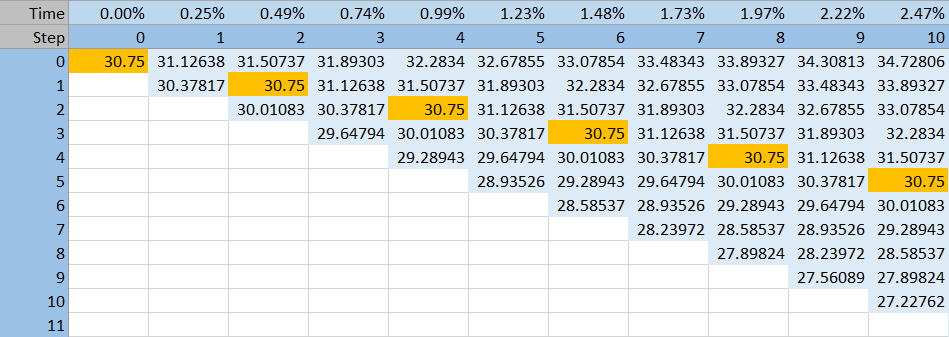
At expiration (at the final model step), prices are still centered around the initial underlying price. In other words, there is no drift in underlying prices in a CRR tree.
Up and down move sizes depend only on volatility and step duration. The formulas are:
UpMove = EXP(VolSQRTStep)
DownMove = 1 / UpMove
... where:
VolSQRTStep = Vol*SQRT(StepPct)
Vol = volatility input in cell C10
StepPct = duration of one step as % of year = time to expiration / number of steps
You can find:
- StepPct in cell C40
- VolSQRTStep in cell C42
- UpMove in cell C45
- DownMove in cell C46
In the UpMove and DownMove IF formulas, the CRR model is the part for Model=1.
Up and Down Move Probabilities
In the CRR model, probability of up and down move is not equal (unlike the Jarrow-Rudd model, where probability of each is 50%).
This is a logical consequence of the CRR up and down move symmetry: If move sizes only consider volatility, but not drift, the latter must be reflected in their probabilities.
In the calculator you can find the probabilities in cells C47 and C48.
Up move probability (CRR is again Model=1 in cell C47 formula) is:
UpProb = (StepCost-DownMove)/(UpMove-DownMove)
... where StepCost is calculated in cell C44 as:
StepCost = EXP((IntRate-Yield)*StepPct)
... where:
IntRate = interest rate input in cell C26
Yield = dividend yield (for stock or index options) or second interest rate (for FX options) in cell C29
StepPct = duration of one step as % of year = time to expiration / number of steps
Because in binomial models there are only two possible paths at any point (up or down), the probabilities of these two must add up to 1 and therefore:
DownProb = 1 – UpProb
Now we have calculated the sizes and probabilities of up and down moves, which is all we need for building the underlying price tree and option price tree.