The Binomial Option Pricing Calculator can work with three different models:
All three models use the same logic for building the binomial trees (for explanation see underlying price tree and option price tree). They differ in the way up and down moves and their probabilities are calculated.
Move Sizes and Probabilities
In general, sizes and probabilities of single step up and down moves depend on volatility and drift of the underlying security.
In other words, they depend on these inputs:
- volatility
- interest rate
- dividend yield (or second interest rate in case of currency options)
Move sizes also depend on the duration of one step, which is time to expiration divided by number of steps. Generally, the longer the single step duration is, the bigger the single step moves are, other things being equal.
You can view step duration, move sizes and probabilities, and other intermediate calculations at the bottom of the main sheet in cells B38-C51.
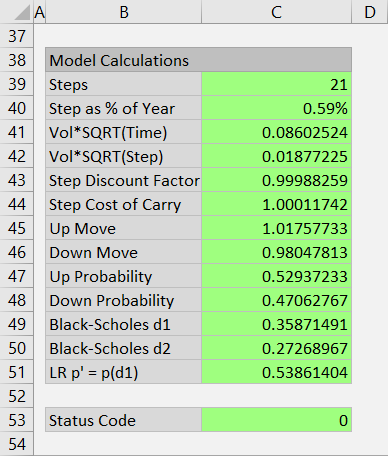
For all three models, probability of up move and probability of down move at each node must add up to 1.
This is due to the very nature of binomial models: At each moment (tree node), there are only two (hence binomial) possible paths for underlying price – up or down – and therefore their probabilities must add up to 100%.
It does not mean the probabilities are always 50%/50% – that is only true for the Jarrow-Rudd model (more details below).
Model Differences
Out of the three models, Cox-Ross-Rubinstein and Jarrow-Rudd are more similar, while Leisen-Reimer is a bit more specific.
Jarrow-Rudd
As already mentioned, under the JR model, probabilities of up and down moves are always 50%/50%.
With the probabilities fixed, all the inputs (volatility, interest rate, dividend yield) must be included in the up and down move sizes.
For more details and formulas see Jarrow-Rudd model.
Cox-Ross-Rubinstein
The CRR model, the most widely known binomial model, takes the opposite approach.
Up and down move sizes depend on volatility, but not on drift (interest rate and yield).
As a result, the product of single step up and down move always equals 1.
In other words, when underlying price moves one step up and one step down, it is back to the original value. Therefore the same prices repeat throughout the underlying price tree. This is a very useful feature, which for instance allows the calculation of option theta directly from the trees.
You can see a CRR underlying price tree below.
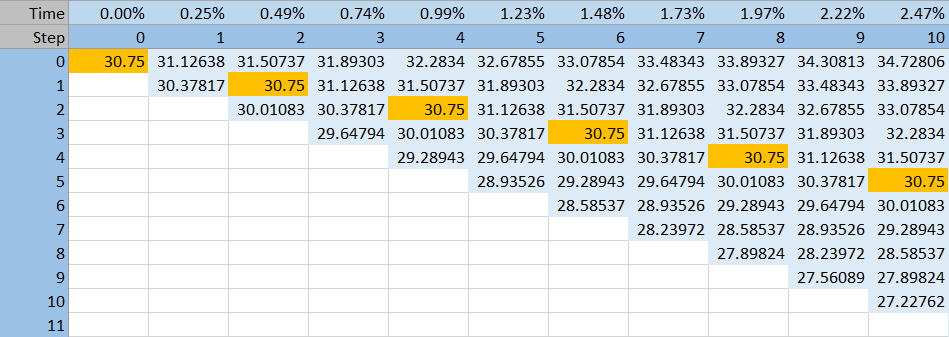
The initial underlying price reoccurs at subsequent steps (orange cells) – generally at all nodes where the path leading to that node includes the same number of up and down moves. The CRR tree is centered around the initial underlying price.
Because the drift (interest rate and dividend yield) is not reflected in the move sizes, it must be included in the probabilities.
For more details and formulas see Cox-Ross-Rubinstein model.
Leisen-Reimer
In the LR model, underlying price at expiration (the final step only, not the entire tree) is centered around the option's strike price.
This is also a very useful feature, which makes the LR model generally more precise with smaller number of steps compared to the two other models.
That said, the number of steps must be odd. The LR model can be very inaccurate with smaller even number of steps.
For more details and formulas see Leisen-Reimer model.
Choosing Model and Number of Steps
Which model and number of steps to use?
The default setting, which in most cases calculates option prices with sufficient accuracy, is Leisen-Reimer model with 21 steps.
While all binomial models generally improve accuracy with increasing number of steps, they also become more resource intensive (can make Excel slow). This is because the number of nodes in binomial trees grows with number of steps squared.
There is a tradeoff between speed and accuracy.
As already mentioned, the Leisen-Reimer model tends to improve accuracy much faster with growing number of steps than the other two models. Unless you need to use a specific model, use Leisen-Reimer for best accuracy and performance.
With Cox-Ross-Rubinstein or Jarrow-Rudd, you may want to use a higher number of steps, like 50.
The calculator supports any number of steps from 2 to 101.
You can change model and number of steps in the Main sheet in cells C3 and C4.