This page explains how to work with option Greeks in the Binomial Option Pricing Calculator.
Where to Find the Greeks
The Greeks are at the top of the Main sheet in the green cells F4-J4, next to the calculated option price.
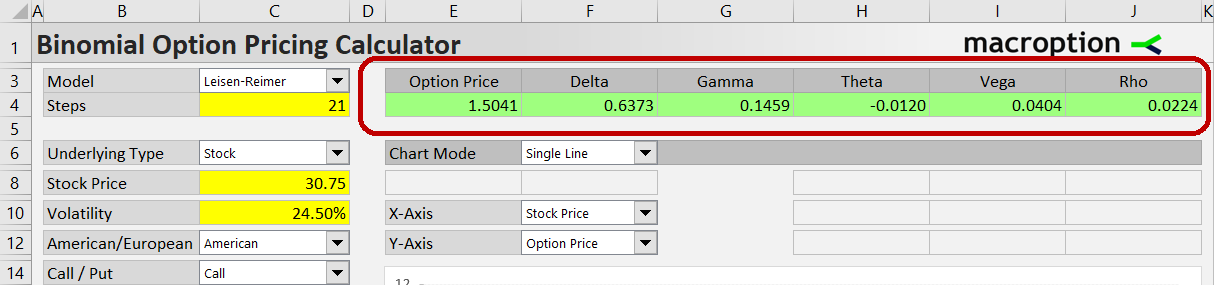
Delta
Delta (cell F4) measures sensitivity of option price to changes in underlying price. Reaching values from -1 (deep in the money puts) to +1 (calls), the value shows the expected change in option price when underlying price increases by 1. The actual change in option price can be slightly different, as delta itself also changes when underlying price goes up or down – that is measured by the next Greek, gamma.
Gamma
Gamma (cell G4) measures sensitivity of delta to changes in underlying price. Its value shows the expected change in delta when underlying price increases by 1.
Theta
Theta (cell H4) measures sensitivity of option price to passing time. With the calculator's default settings, its value shows how the option will change in one day (as time to expiration decreases by one day). You can change theta units and sign in the Preferences sheet (the settings named ThetaPeriods and ThetaSign) and make theta show expected option price change per week instead or per day, for example.
Vega
Vega (cell I4) measures sensitivity of option price to changes in volatility. Generally, options are more valuable with greater volatility. The vega value shows how the option price is expected to change when volatility increases by one percentage point.
Rho
Rho (cell J4) measures sensitivity of option price to changes in interest rate. As with vega and volatility, the rho value shows how much the option price will change when the risk-free interest rate increases by one percentage point.
Charting the Greeks
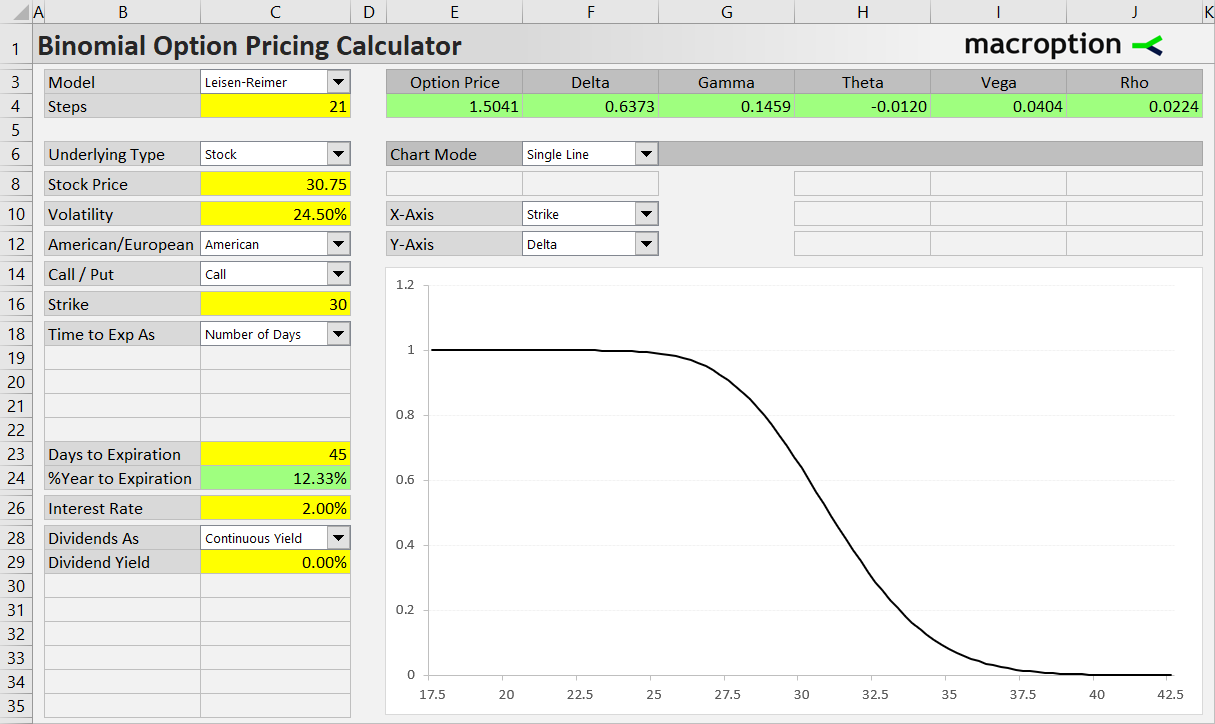
You can display any of the Greeks on the chart's Y-axis and model how it is affected by the individual inputs (in the chart's Single Line mode) or a combination of them (in the Scenario Analysis mode).
For instance, you can show deltas for different strikes.
Or, in Scenario Analysis, you can model how the option's gamma will change with stock price, depending on which strike you choose.
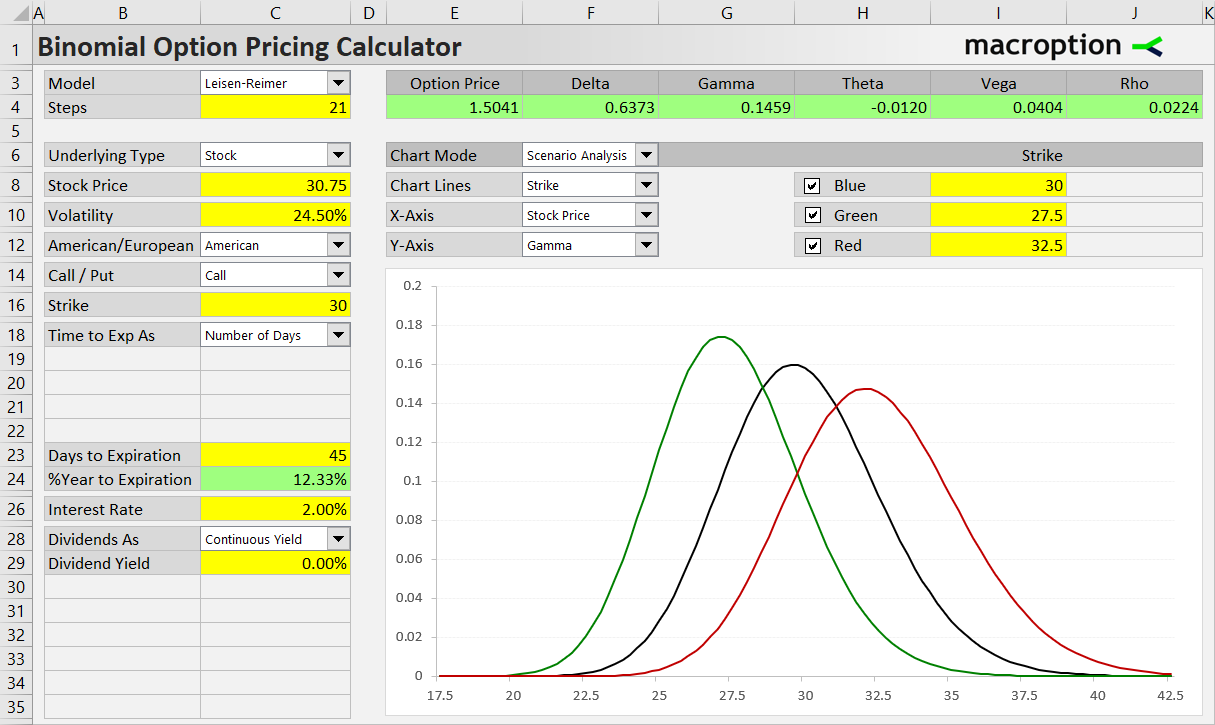
Any combination of inputs and Greeks will work.
How Binomial Models Calculate the Greeks
With binomial models, some of the Greeks can be calculated in two different ways.
Calculating Greeks from Binomial Trees
The easier and faster method is to calculate the Greeks directly from different nodes of the binomial trees. It works for delta, gamma, and sometimes (in the Cox-Ross-Rubinstein model) for theta.
Delta can be calculated from the two nodes in step 1 (one step up and one step down from the initial underlying price) as the difference between option prices divided by the difference in underlying prices.
Gamma can be calculated as the difference between deltas at the two nodes in step 1 divided by the difference in underlying prices. The delta at each step 1 node is calculated again as difference in option prices divided by the difference in underlying prices, this time using step 2 nodes (always the node up and down from the particular step 1 node).
Theta can be calculated as the difference in option prices between the initial (step 0) node and the middle node of step 2, divided by 2x the duration of one step. The precondition is that underlying price must be the same at the two nodes, which is only true under the Cox-Ross-Rubinstein model, where the product of one up move and one down move equals 1 and therefore the same underlying prices reoccur on subsequent nodes. With the other two models this does not happen and theta can't be calculated directly from the trees.
Calculating Greeks by Incrementing Inputs
The second method works for all the Greeks under all the models. For each of the Greeks, two option prices are calculated using the same values for all inputs except the one whose effect the particular Greek measures (underlying price for delta, time for theta, volatility for vega, interest rate for rho). The resulting Greek value is the difference between the two option prices divided by the difference between the two values of the variable input.
For example, to calculate delta, option prices at two different underlying prices must be calculated, other inputs being the same. If the resulting option prices are 1.50 at underlying price 30 and 1.70 at underlying price 31, the resulting delta (valid at underlying price 30.50) is:
(1.70 – 1.50) / (31 – 30) = 0.20
Note that the distance of the variable input values (how close or far apart they are) can affect results. For instance, you can calculate delta at underlying price 30.50 from option prices at 30 and 31, or 30.40 and 30.60, or 30.49 or 30.51. There is no perfect distance (accuracy depends on model, number of steps and values of the other inputs). The calculator uses distance of 2% (one option price 1% up from the current input, the other 1% down; it is percent, not percentage points, also for volatility and interest rate) – delta at underlying price 30.50 would be calculated using option price at 30.19 and 30.81 (30.50 plus or minus 0.3050).
Most users don't need to worry about the details of these calculations – just be aware there are two methods you can use.
Selecting the Calculation Method
Often the second method is more accurate than calculating Greeks directly from binomial trees, but it is more computationally expensive, because it generates two entirely new sets of binomial trees (four for gamma, which requires calculation of two deltas). This can be very slow especially with high number of model steps and when one of the Greeks is displayed in the chart (in that case you are calculating that Greek for every point on the chart, which requires a lot of binomial trees).
By default, the Binomial Option Pricing Calculator calculates delta, gamma and theta (when possible) directly from trees and the other Greeks by incrementing inputs. You can select the calculation method for delta, gamma and theta in the Preferences sheet, by setting the cells DeltaFromTree, GammaFromTree, ThetaFromTree to TRUE or FALSE.