This page explains how to price futures options in the Binomial Option Pricing Calculator.
Entering Inputs
To price futures options, select "Futures" in the Underlying Type dropdown box in cell C6.
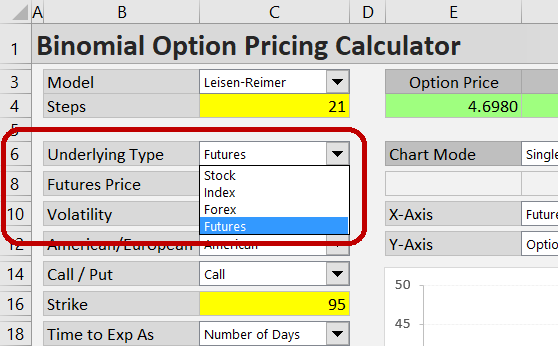
Set the individual inputs in the cells below (C8-C26). Most of them work just like with the other underlying types (see the general instructions for entering inputs). Some futures option inputs may need further explanation.
Underlying Price
When pricing futures options, binomial models use the futures price, not the spot price, as underlying price. The term underlying price can be a bit confusing in this case (the spot is the ultimate underlying for both the futures and the futures options), which is also why the label of the underlying price input (cell B8) shows "Futures Price" when "Futures" is selected as underlying type.
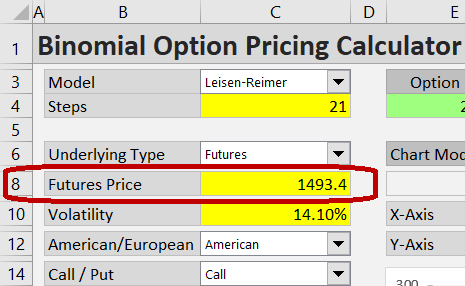
Enter the current futures price in the yellow cell C8.
Time to Expiration
Time to expiration, entered in cells C18-C24 (details here), refers to the expiration of the option, not the expiration of the futures contract.
Futures options and their underlying futures contracts often expire at the same time, but sometimes the options expire earlier. For instance, when the futures expiration cycle is quarterly and the options expirations are monthly, options on a March futures contract can expire in January, February and March. It is always the option expiration that enters the option pricing model. The futures expiration date does not affect the calculations in any way.
Interest Rate
Interest rate, entered in the yellow cell C26, is just like interest rate for the other underlying types. Enter the continuously compounded risk-free interest rate, with the interest rate tenor (time to maturity) roughly matching the time to option expiration.

How Binomial Models Price Futures Options
The way binomial models work with interest rate is quite specific with futures options, due to the added relationship between interest rate, spot price and futures price.
As option underlying, from the perspective of option pricing models (not only binomial models, but also Black-Scholes / Black 76 model, for instance), a futures contract is just like a stock that pays continuous dividend yield equal to the risk-free interest rate. Therefore, with futures options, the risk-free interest rate enters the calculations in two places – as interest rate and as continuous yield (in the same place as dividend yield for stock options or foreign interest rate for currency options).
Therefore, the Yield input cell (C29) is hidden when Futures is selected as Underlying Type, but it is not zero – it is set equal to the risk-free interest rate in cell C27.
Futures Options Pricing Example
As an example, let's price a call option on gold futures. The underlying futures contract is currently trading at 1493.40. This is the underlying price input for the pricing model (cell C8). Spot gold price does not enter the calculations in any way.
The call option is American, has 1500 strike price and expires in 36 days. Time to expiration to use as the model's input is time to the option's expiration, not time to expiration of the futures contract (these are the same sometimes, but often different).
We also need to enter the remaining inputs: volatility (14.10% in cell C10) and risk-free interest rate (2.00% in cell C26).
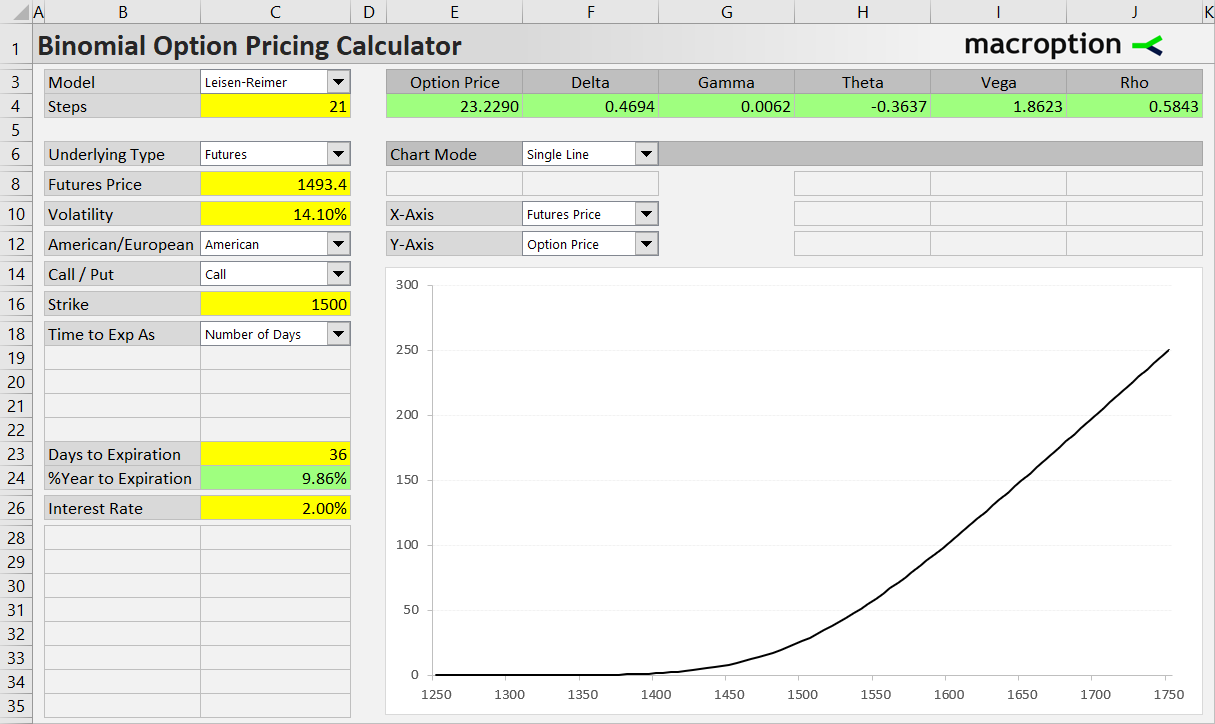
The resulting option price is $23.23 (cell E4). You can also see the Greeks in the other green cells.
In the chart you can model effects of futures price and all the other inputs on the option price or any of the Greeks.
Other Underlying Types
For instructions and examples for the other underlying types, see: