This page explains the implementation of Jarrow-Rudd model in the Binomial Option Pricing Calculator.
All three models supported by the calculator – this one, Cox-Ross-Rubinstein and Leisen-Reimer – follow the same logic for constructing binomial trees (that part is explained in underlying price tree and option price tree).
The models only differ in sizes and probabilities of underlying price up and down moves in the underlying price tree. Jarrow-Rudd calculations of these are explained below.
You can find these calculations in the Model Calculations section at the bottom of the Main sheet, in cells B38-C51.
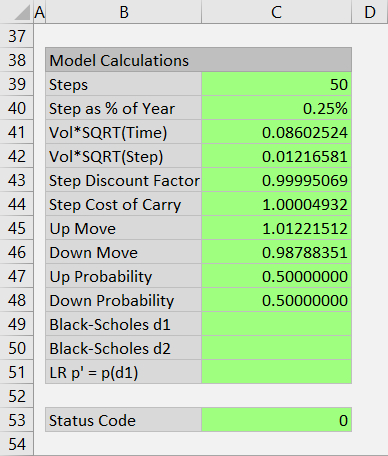
Up and Down Move Probabilities
In Jarrow-Rudd binomial trees, price always has the same probability (50%) of going up or down from the current to the next step.
UpProb = DownProb = 0.5
These probabilities are in cells C47 and C48.
Up and Down Move Sizes
With the probabilities fixed, all the inputs that normally affect price moves – volatility, interest rate and yield – must be reflected in the move sizes. The formulas are:
UpMove = EXP((IntRate-Yield-0.5*Vol^2)*StepPct+VolSQRTStep)
DownMove = EXP((IntRate-Yield-0.5*Vol^2)*StepPct-VolSQRTStep)
The up and down move formulas are almost the same.
The only difference is the sign before the last part (VolSQRTStep), which is a product of volatility and square root of step duration:
VolSQRTStep = Vol*SQRT(StepPct)
StepPct = step duration as % of year = time to expiration / number of steps
You can find StepPct in cell C40 and VolSQRTStep in cell C42.
Generally, the greater volatility and step duration, the greater the difference between single up and down move size.
The remaining (first) part of the EXP function argument is the same for up and down move and reflects underlying price drift:
(IntRate-Yield-0.5*Vol^2)*StepPct
... where:
- interest rate in cell C26
- yield in cell C29 (dividend yield for stock or index options, or second interest rate for currency options)
- volatility in cell C10
Because all the above inputs are entered annualized, the entire expression IntRate-Yield-0.5*Vol^2 must be converted to a single step return by multiplying it by StepPct, which is already familiar.
Now we have calculated the sizes and probabilities of up and down moves, which is all we need for building the underlying price tree and option price tree.