This page explains iron condor profit or loss at expiration and the calculation of its maximum profit, maximum loss, break-even points and risk-reward ratio.
Iron Condor Basic Characteristics
Iron condor is a non-directional short volatility strategy with limited risk and limited profit potential. It got its name from the shape of its payoff diagram, which resembles a condor with wide wingspan:
The position involves four options with four different strikes, all with the same expiration date:
- Long put, whose strike is the lowest of all the legs.
- Short put with a strike higher than the long put.
- Short call with a strike higher than the short put.
- Long call, whose strike is the highest of all.
The order of strikes matters – from lowest to highest it is: long put, short put, short call, long call.
Let's use an example to explain the different profit or loss scenarios and calculate maximum profit, maximum risk, break-even points and risk-reward ratio.
Iron Condor Example
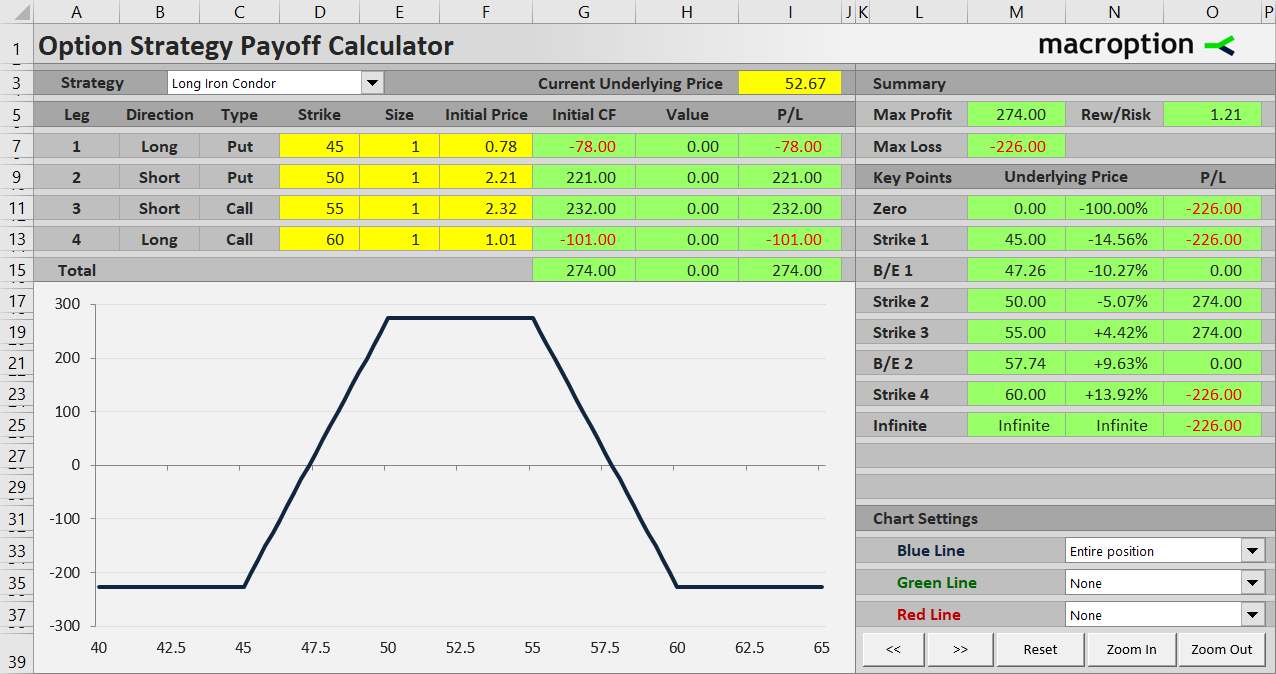
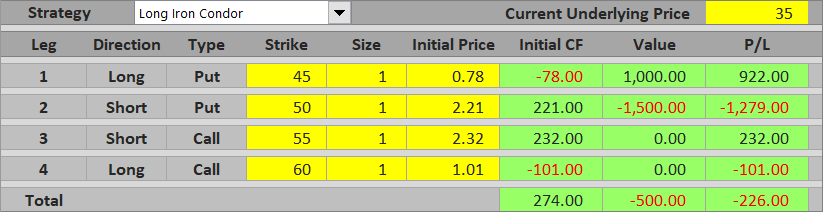
Let's set up an iron condor position by the following four transactions:
- Buy a $45 strike put option for $0.78 per share.
- Sell a $50 strike put for $2.21.
- Sell a $55 strike call for $2.32.
- Buy a $60 strike call for $1.01.
The middle two short options are sometimes called the body of the condor, while the long outer strikes are called wings. When entering an iron condor trade, make sure both wings have the same width. In other words, the distances between the two put strikes (55 – 45 = 5 in our example) and the two call strikes (60 – 55 = 5) should match. This makes the position non-directional with equal risk on both sides (a variation with uneven wing width and directional bias is called broken wing iron condor).
The width of the body can be different, although in our example it is 55 – 50 = also 5.
Initial Cash Flow
Iron condor is a credit strategy – initial cash flow is positive, because the inner strike put and call which you sell are more expensive than the outer strike put and call which you buy.
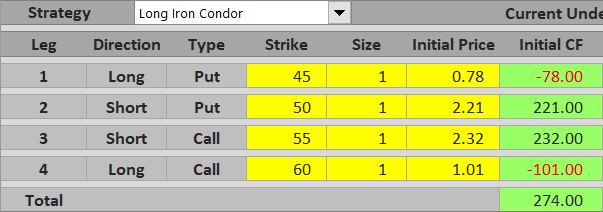
In our example, assuming one contract which represents 100 shares of the underlying, initial cash flow is:
- $78 paid for the long put
- $221 received for the short put
- $232 received for the short call
- $101 paid for the long call
We receive $453 for the short legs and pay $179 for the long legs. Net premium received is $274.
In general:
Iron condor initial cash flow = short put premium received + short call premium received – long put premium paid – long call premium paid
Maximum Profit
The objective of an iron condor trade is to defend the premium – ideally keep all the cash we have received in the beginning without being assigned any of the short options.
For example, if the underlying ends up at $52 at expiration, all the options expire worthless and there is no further change to overall P/L. We keep the net premium received ($274).
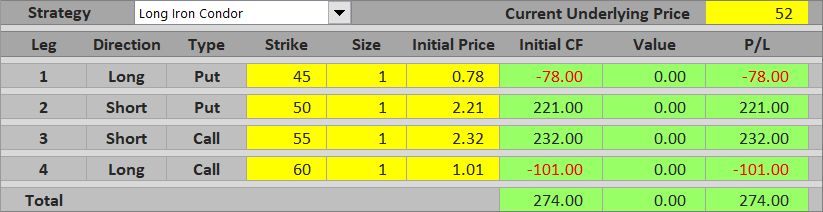
Maximum profit from an iron condor trade equals net premium received. It applies when underlying price ends up between the inner (short) strikes at expiration (or exactly at one of them).
Between the Call Strikes
When underlying price gets above the short call strike, the short call gets in the money. We will be assigned this option at expiration and its value will be our loss. If it is smaller than initial cash flow, the overall result will still be a profit, although smaller than maximum profit.
For instance, if underlying price ends up at $56, the short call is worth $56 – $55 = $1 per share = $100 for one contract at expiration. All the other options expire worthless. Total P/L from the iron condor is $274 – $100 = $174.
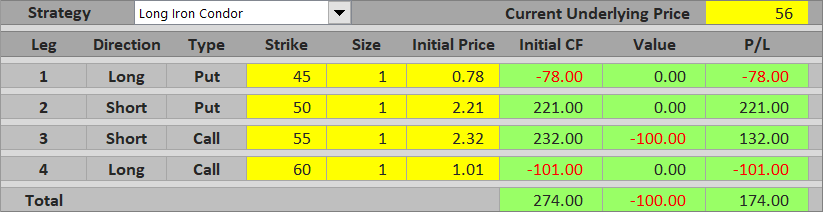
If the underlying gets high enough that the short call option's value exceeds initial cash flow, total P/L is a loss.
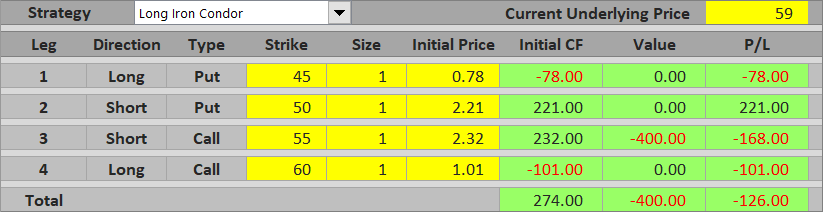
The general formula for total P/L when underlying price end up between the two call strikes is:
P/L = net premium received – short call value
P/L = net premium received – (underlying price – short call strike)
Above the Highest Strike
Once the underlying gets above the long call strike, both call options are in the money. Further increase in (the negative) value of the short call is offset by increase in the long call value. The effects of the two calls cancel one another and their combined value is constant, equal to the difference between their strikes (in our case $60 – $55 = $5 per share = $500 per contract). Total P/L is a loss, because this difference is greater than net premium received.
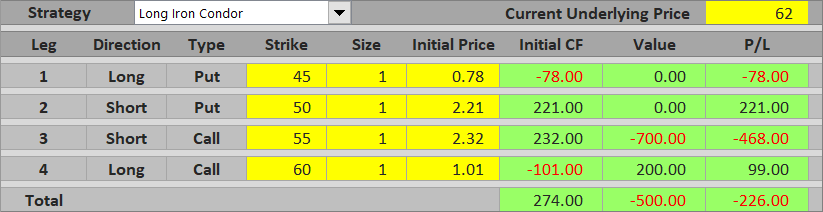
The general formula for P/L above the long call strike is:
P/L = net premium received – difference between call strikes
P/L = net premium received – (long call strike – short call strike)
In our example:
P/L = $2.74 – ($60 – $55) = $2.74 – $5 = – $2.26 per share = – $226 per contract
Between the Put Strikes
When underlying price ends up between the two put strikes at expiration, we are assigned the short put, whose value reduces our profit. If it's smaller than net premium received, overall P/L is still positive.
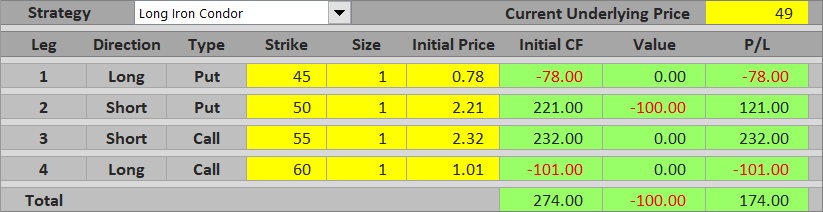
If the short put's value exceeds initial cash flow, the iron condor loses money overall.
The general formula is:
P/L = net premium received – short put value
P/L = net premium received – (short put strike – underlying price)
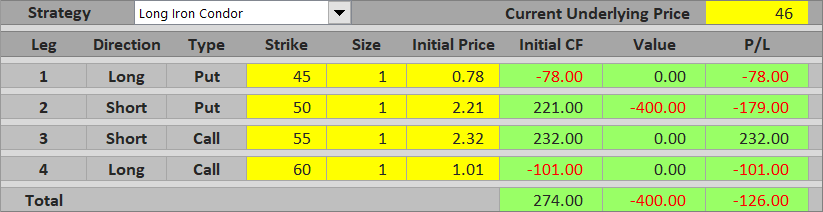
Below the Lowest Strike
Below the long put strike, the effects of the two put options cancel each other and their combined value is constant, equal to difference between their strikes, like with the calls above the highest strike.
P/L = net premium received – difference between put strikes
P/L = net premium received – (short put strike – long put strike)
In our example:
P/L = $2.74 – ($50 – $45) = $2.74 – $5 = – $2.26 per share = – $226 per contract
As you can see, if both wings have the same width (difference between call strikes equals difference between put strikes), P/L is exactly the same above the highest strike and below the lowest strike. This is the maximum possible loss from the trade.
Iron Condor Risk-Reward Ratio
Because we already know maximum profit ($274) and maximum loss ($226), we can calculate the risk-reward ratio. It is 1 : 274/226 or 1 : 1.21. In other words, potential profit from the iron condor in our example is 1.21x the risk.
The general formulas (for an iron condor with equal width of the two wings) are the following:
Maximum profit (reward) = net premium received
Maximum loss (risk) = net premium received – difference between put strikes
Maximum loss (risk) = net premium received – difference between call strikes
Difference between put strikes = difference between call strikes = maximum profit + maximum loss
Iron Condor Break-Even Points
The iron condor strategy has two break-even points: one between the put strikes and one between the call strikes.
The first break-even is the underlying price where the short put option's value equals initial cash flow.
B/E #1 = short put strike – net premium received
The other is where the short call option's value equals initial cash flow.
B/E #2 = short call strike + net premium received
In our example the break-evens are:
B/E #1 = $50 – $2.74 = $47.26
B/E #2 = $55 + $2.74 = $57.74
Iron Condor Payoff Summary

Maximum profit equals net premium received and applies between (or exactly at) the inner strikes.
Between the call strikes and between the put strikes total P/L declines as underlying price gets further away from the short call or short put strike.
Maximum loss applies above the highest strike or below the lowest strike.
Iron Condor as Combination of Other Strategies
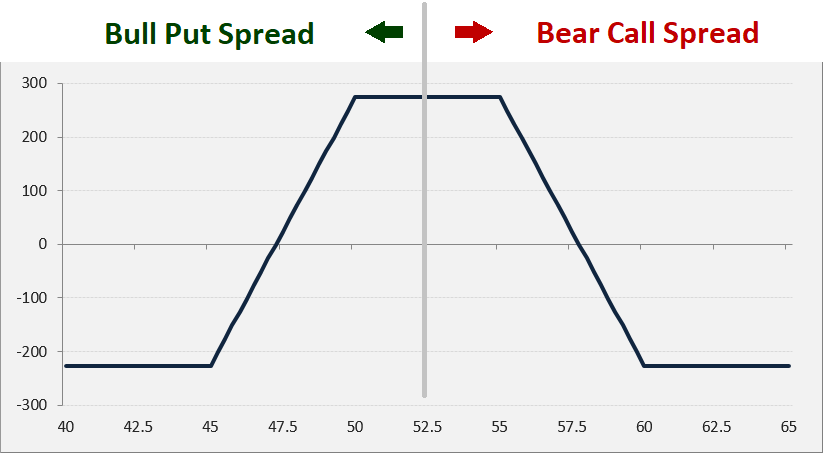
If you are familiar with other option strategies, you might have noticed that iron condor is actually a combination of two vertical spreads – a bull put spread (long lower strike put + short higher strike put) and a bear call spread (short lower strike call + long higher strike call). Profit or loss from an iron condor can be calculated as sum of P/L of these two strategies. The payoff diagram looks like a bull put spread and a bear call spread payoff diagrams placed next to one another.
Alternatively, you can see iron condor as a combination of short strangle (short put + short call) and long strangle (long put + long call).
Strategies with Payoff Similar to Iron Condor
While iron condor user both puts and calls, you can actually create the same payoff profile using only calls or only puts. These strategies are known as call condor and put condor.
Iron condor payoff is similar to iron butterfly. The main difference is that in an iron butterfly the short put and the short call have the same strike (because butterflies have much smaller bodies than condors). As a result, initial cash flow (maximum possible profit) from an iron butterfly tends to be higher compared to iron condor, but its profit window (distance between break-even points) is narrower. Other things being equal, iron butterfly has better risk-reward ratio but lower probability of profit than iron condor.