Leisen-Reimer Model Formulas

This page explains formulas used in Leisen-Reimer binomial option pricing model.

For similar pages for other models see Cox-Ross-Rubinstein, Jarrow-Rudd.

For implementation of these formulas in Excel see Leisen-Reimer Model in Excel.

Leisen-Reimer Model Logic

This model was introduced by Dietmar Leisen and Matthias Reimer in 1995 (in a paper titled Binomial Models for Option Valuation – Examining and Improving Convergence, published in Applied Mathematical Finance, 3, 319-346).

Its main benefit is greater precision with smaller number of steps, compared to earlier models such as Cox-Ross-Rubinstein (CRR) or Jarrow-Rudd (JR).

Convergence

Generally, all binomial models become more precise (converge to continuous model solutions like Black-Scholes) with growing number of steps, as the duration of each step becomes shorter. This convergence is not always smooth – with models including CRR and JR, it oscillates (try incrementing number of steps in a calculator and watch how the calculated option price behaves).

In practical use, where higher number of steps requires more computing resources, desired qualities of a binomial model are for the convergence (precision improvement) to be fast and smooth.

This is where Leisen-Reimer model provides a good solution.

Tree Centered around Strike

Its main idea is that the underlying price binomial tree is centered around the option's strike price at expiration (not around the current underlying price like CRR).

The logic and calculation of tree nodes and option price is the same as in other binomial models – for detailed explanation see How Binomial Trees Work.

The difference is only in the calculation of tree parameters (up and down move sizes and probabilities), which I explain below.

Binomial Tree Probabilities

In Leisen-Reimer model, probabilities must be calculated before move sizes, because the former are inputs for the latter.

But first we need to calculate d₁ and d₂, which may be familiar from the Black-Scholes model (the formulas are the same):

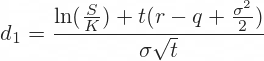
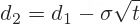
... with the six usual option pricing inputs:

• S is current underlying price
• K is option's strike price
• t is time to expiration in years
• r is risk-free interest rate
• q is continuous dividend yield (or foreign interest rate with currency options)
• σ is volatility

Now we can use d₂ to calculate the probability of up move in a Leisen-Reimer tree:

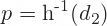
Peizer-Pratt Inversion

h^-1(z) is the Peizer-Pratt inversion function, which provides (discrete) binomial estimates for the (continuous) normal cumulative distribution function. There are alternative formulas for this function, listed below.

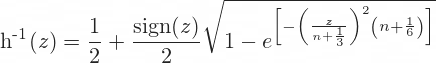
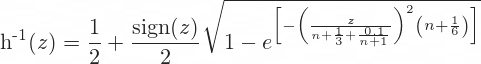
The second is a bit more precise. The only difference is the extra 0.1/(n+1).

When using these formulas to calculate p = h^-1(d₂), use d₂ in place of z.

n is number of steps of the binomial model. One restriction of Leisen-Reimer model is that number of steps must be odd. An even n will not break the calculations, but it leads to imprecise option prices.

The calculated p is the probability of up move. Probability of down move is 1 – p.

Binomial Tree Move Sizes

The Leisen-Reimer up and down move size formulas are:

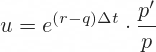
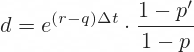
The exponent term e^(r-q)Δt should look familiar. It can be interpreted as net cost of holding the underlying security over one step, as Δt is the duration of one step in years, calculated as t/n.

In each formula this term is multiplied by a ratio of two probabilities, p' and p for up move, and 1 – p' and 1 – p for down move, as one would expect.

We already have p, but p' is new. We can calculate it using the same Peizer-Pratt formula as p, this time using the Black-Scholes d₁ (instead of d₂) as argument:

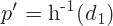
This p' is only used here, to calculate u and d. In the rest of the model (when calculating option price tree nodes) we always use p.

Binomial Trees and Option Price

Now we have up and down move sizes and probabilities, which we can use to calculate all nodes in the underlying price tree and option price tree, and eventually the current option price, which is the model's output.

This part is the same as in other binomial models. You can find detailed explanation and formulas here:

How Binomial Trees Work

For Excel implementation see:

Leisen-Reimer Model in Excel