This page explains formulas used in Cox-Ross-Rubinstein binomial option pricing model.
For similar pages for other models see Jarrow-Rudd, Leisen-Reimer.
For implementation of these formulas in Excel see Cox-Ross-Rubinstein Model in Excel.
Cox-Ross-Rubinstein Model Logic
All binomial option pricing models share the same logic of simulating underlying price moves in underlying price binomial tree and calculating option price from option price tree. This logic is explained here: How Binomial Trees Work.
Individual binomial models differ in the exact way how the underlying price tree is built. In other words, in the exact calculation of up and down move sizes and probabilities.
A special characteristic of Cox-Ross-Rubinstein model is that the product of up and down move is 1.
u · d = 1
u = 1 / d
d = 1 / u
... where u is the up move multiplier and d is the down move multiplier.
In other words, if price moves up one step and then down one step (or down one step and then up one step), it returns to its original level.
For example, if up move multiplier u is 1.25 (price goes up 25%), down move multiplier d must be 1 / 1.25 = 0.8 (price goes down 20%). Note that the percentages are not equal, but the product u · d = 1.
This relationship, unique to Cox-Ross-Rubinstein model, has important implications for the binomial tree:
- The underlying price tree is symmetric around the initial underlying price.
- The same prices keep reoccurring in subsequent steps. This, among other things, allows estimating option theta directly from Cox-Ross-Rubinstein trees (it is not possible under other models).
Binomial Tree Up Move
The Cox-Ross-Rubinstein formula for up move multiplier is:

... where σ is volatility and Δt is duration of one step in years, calculated as:
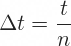
... where t is time to expiration in years (days to expiration divided by 365) and n is number of steps used in the model.
Binomial Tree Down Move
We have already explained that
d = 1 / u
Alternatively, down move multiplier can be calculated directly as:

The only difference from the up move formula is the minus sign. Therefore the product u · d must equal 1.
Binomial Tree Probabilities
It is clear from the formulas above and from the logic of tree symmetry that Cox-Ross-Rubinstein up and down moves don't reflect price drift. They only reflect volatility σ. Drift factors such as interest rate r and yield q do not enter the move size formulas in any way.
Therefore they must be reflected in the probabilities.
Cox-Ross-Rubinstein up move probability formula is:
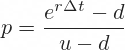
With dividend yield (or foreign interest rate when pricing currency options) the probability formula is:
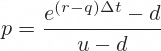
Down move probability is of course 1 – p, because up and down move probabilities must add up to one.
Calculating Binomial Trees
The move sizes calculated above are used to calculate prices in individual nodes of the underlying price tree. The probabilities are used to calculate the option price tree and eventually the current option price, which is the model's output.
These calculations are the same for different binomial option pricing models. For detailed explanation and formulas see:
For Excel implementation see: