This page explains the strike price input in the Black-Scholes option pricing model and the effect of strike selection on option prices and Greeks.
Strike Price as Black-Scholes Input
The Black-Scholes option pricing model takes five inputs which determine the values of call and put options. These inputs are underlying price, strike price, time to expiration, volatility, and interest rate (and dividend yield as sixth input in Merton's extension of the model).
Strike price, also called exercise price, is the price at which you can buy the underlying security when exercising a call option, or at which you can sell the underlying when exercising a put.
Strike price is not to be confused with underlying price, which is another input of the model, or with the option's market price (premium), which is the output (for more detailed explanation see Strike Price vs. Underlying Price vs. Option Premium).
As a Black-Scholes input, strike price has one unique characteristic that differentiates it from all the other inputs: for a particular option, strike price is fixed and doesn't change throughout the option's life. It is one of the key contract specifications of the option. For example, we can speak of a "30 call", which means a call option with strike price of $30, or in other words a call option that enables its owner to buy the underlying stock at $30 per share when exercised.
Strike Selection
When considering a potential option trade, one of the most important decisions is which strike to choose. This selection can have substantial effect on both risk and profit potential of the trade.
Therefore it is essential to understand how strike price affects option prices – not only on its own, but also in combination with the other factors like time to expiration or volatility, which change throughout an option's life. The Black-Scholes model can help us understand and model these effects, and thereby help us select the best option for a particular trading idea.
Call Option Strike Price Effects
The value of any option depends on the relationship between strike price and underlying price.
Calls, which provide a right to buy the underlying security at a fixed price (the strike price), are the more valuable, the more underlying price exceeds strike price.
You can see the effect strike price has on call option price (premium) when looking at the Black-Scholes call formula:
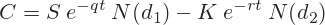
S0 denotes the current underlying price and X denotes the option's strike price (sometimes the letter K is used for strike instead of X).
Call option premium is inverse to strike price. The lower the strike price, the higher the premium, given the same underlying price.
However, this relationship is not linear. Both S0 and X are multiplied by a number of other factors, whose values depend on the other Black-Scholes inputs (for detailed explanation see Black-Scholes formula). When underlying price exceeds strike price by a wide margin (the call is deep in the money), both S0 and X are multiplied by a number close to positive one, the resulting option premium approaches S0 minus X, and the relationship becomes close to linear.
Example
Let's say you are thinking a stock might go up in the next two months, but you don't want to take the risk of buying the stock itself. You want to buy a call option instead. The stock is currently trading at $100 per share in the stock market (this is the underlying price S0). You are deciding which strike (X) to buy.
In the chart below, the upper green line shows the premiums of call options with different strike price (assuming underlying price $100, 60 days to expiration and implied volatility 25%). The lower blue line shows the option's delta (sensitivity to changes in underlying price).
The low strike options are the most expensive, because the underlying price S0 exceeds their strikes X by the widest margin. They have high intrinsic value (the positive difference between S0 and X) and relatively small time value. Therefore they are very sensitive to changes in intrinsic value, or changes in underlying price, and delta is close to +1.
In the middle of the X-axis, where strikes are close to the current underlying price ($100 in our example), intrinsic value is relatively small (for strikes below $100) or zero (for strikes at and above $100), but time value is high. Both intrinsic value and delta decrease as we move to higher strikes.
On the right end of the X-axis, strike prices exceed the current underlying price by a wide margin and option premiums approach zero. Intrinsic value is zero. Time value is approaching zero, as the possibility of the options ever getting in the money (underlying price rising above the strike) is very small. Delta is also approaching zero, as the options are quite insensitive to underlying price changes.
When deciding which strike to choose for a particular trade, you can use delta as a simple measure of an option's sensitivity to changes in underlying price. If you want an option that moves a lot as underlying price changes, choose a lower strike and higher delta option. That said, such option will also be more expensive. If you want to get exposure to the underlying at low cost and low risk, or with greater leverage, choose a higher strike option, whose delta is smaller at the moment, but may increase if you are right about the underlying price direction.
Put Option Strike Price Effects
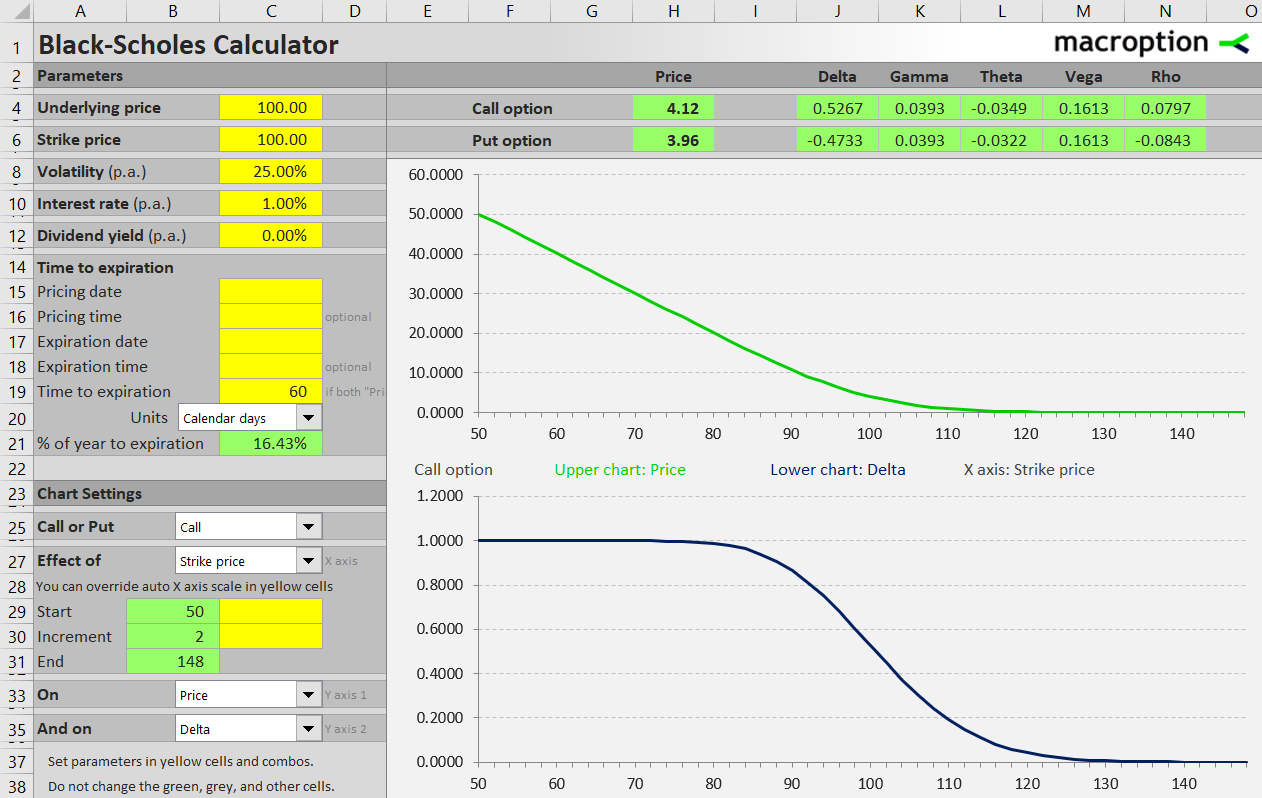
The effect of strike price on put options is very similar to calls – just inverse, because a put represents the right to sell, rather than buy the underlying security at the strike price.
In the Black-Scholes put premium formula the order of S0 and X is reversed.
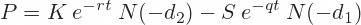
A put is the more valuable, the more strike price exceeds the current underlying price.
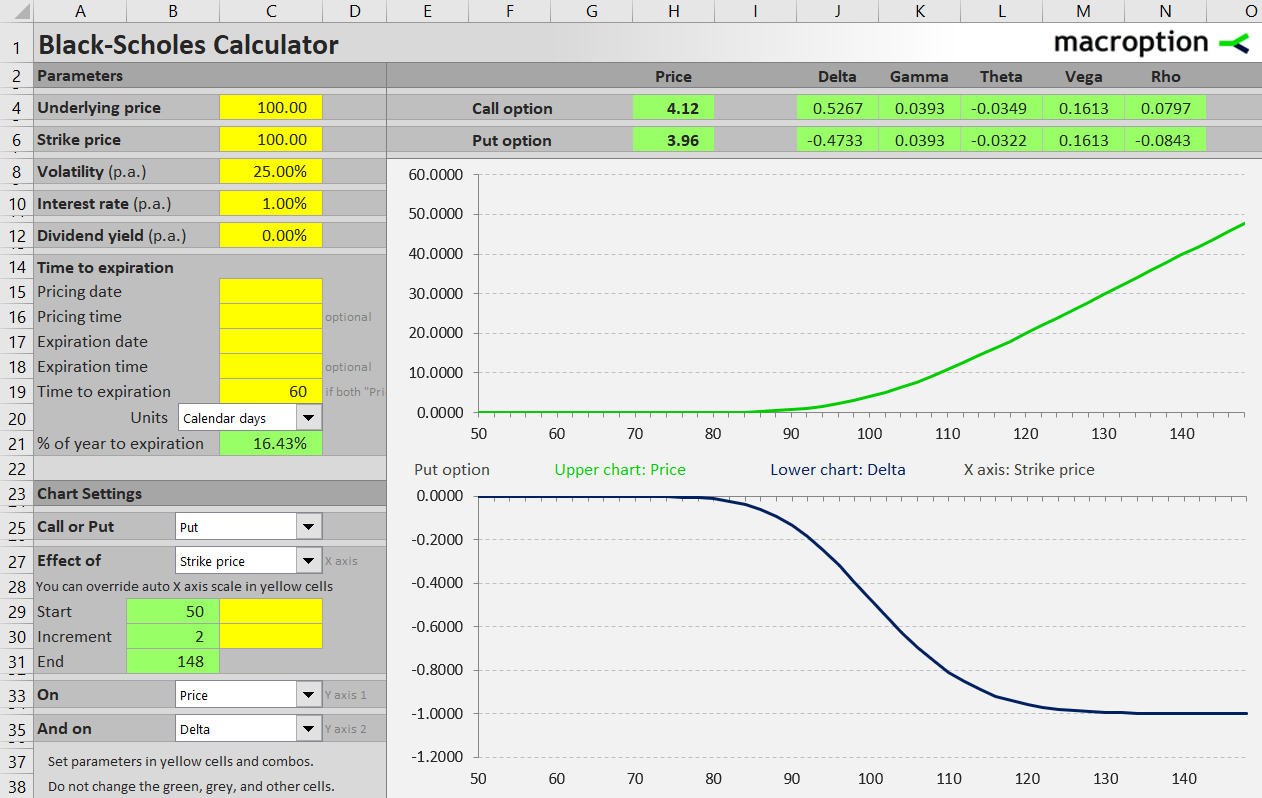
High strike puts are the most valuable and also most sensitive to changes in underlying price. Delta is approaching -1 (because a put's value decreases as underlying price rises).
Conversely, low strike puts are out of the money and their deltas approach zero.
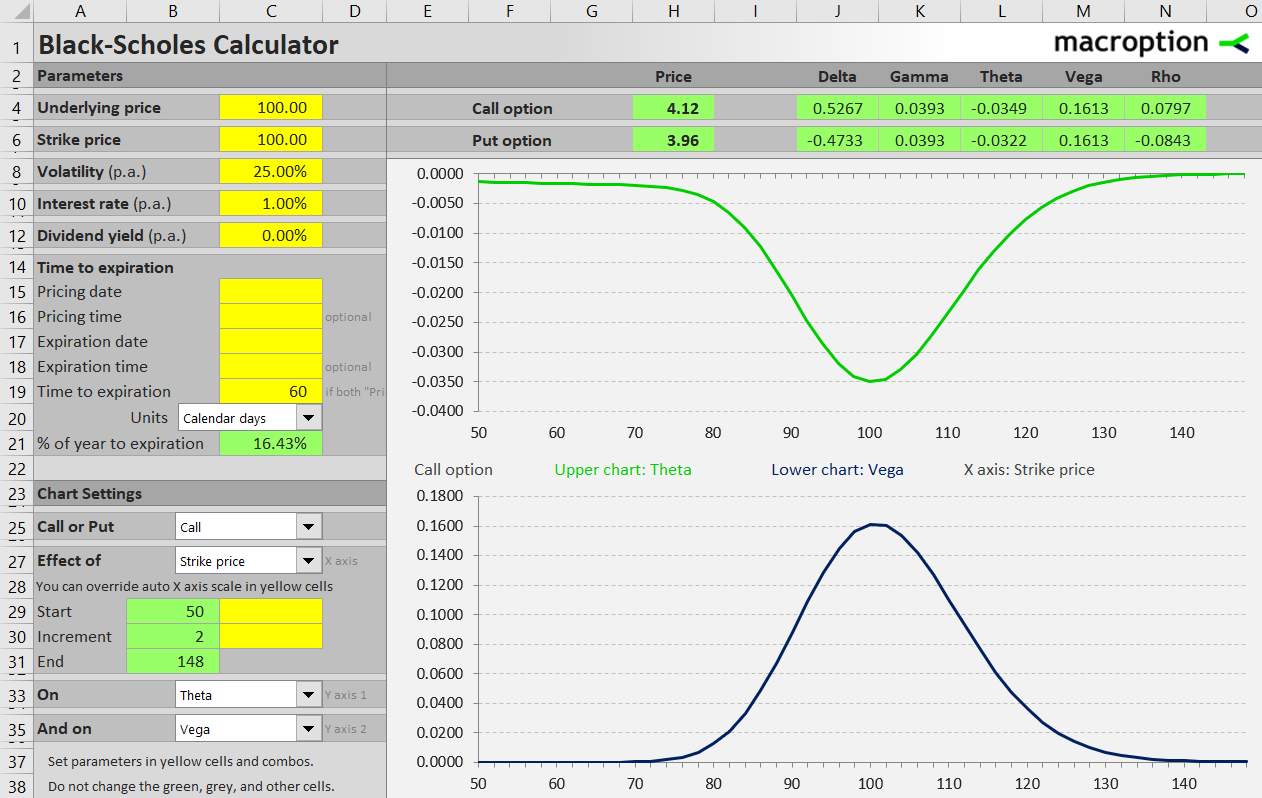
Effect of Strike Price on Theta and Vega
Strike price affects not only how an option's price changes with underlying price, but also the option's sensitivity to other factors. For example, with passing time some strikes will lose value faster than others. Different strikes will also react differently to changes in volatility.
The chart below shows the effect of call option strike selection on theta (which measures how fast an option loses value with passing time) and vega (which measures sensitivity to volatility changes). We are using the same set of options from the earlier example (underlying price $100, 60 days to expiration, implied volatility 25%). Both time and volatility have the greatest impact on at the money options – the strikes close to the current underlying price. It is similar for put options.
For detailed instructions for drawing these charts see Working with Strike Price in the Black-Scholes Calculator.
For overview of all the calculator's features and more screenshots, see Black-Scholes Calculator.