This page explains the underlying price input in the Black-Scholes option pricing model and the effects of underlying price changes on call and put option prices.
Underlying Price and Option Premium
Underlying price is one of the five/six inputs in the Black-Scholes option pricing model (the others are strike price, volatility, time to expiration, risk-free interest rate, and – under Merton's dividend extension – dividend yield). Underlying price is one of the most important inputs, and one that often has the greatest effect on option prices. After all, the very reason why one would buy an option is to hedge against unfavorable underlying price changes (e.g. buy puts as protection against a possible stock price decline), or to profit from favorable ones (e.g. buy a call hoping for a stock to rise).
An option is a derivative security, which means it is derived from another security, such as a stock. This stock is called the underlying security for the option, or simply the underlying. The stock's price is the underlying price. The option's price, also called option premium, is derived from the underlying stock's price.
Underlying price is not to be confused with strike price, which is another input of the Black-Scholes model. Strike price is the price for which you can buy the underlying security if you choose to exercise a call option, of for which you can sell the underlying when exercising a put. The relationship between underlying price and strike price is the key factor determining an option's price (premium) and the key part of Black-Scholes option price formulas.
For understanding and trading of options, it is essential that one understands the difference between these three prices: underlying price (price of the stock), option premium (price of the option), and strike price (price paid for the stock if option is exercised).
What to Use as Underlying Price Input
When pricing an option using the Black-Scholes model, the number to use in the underlying price input is the current price of the underlying stock.
For example, when you are calculating the price of an option on the Apple stock, the number to enter is the latest Apple stock price.
When pricing an option on the S&P500 index, use the latest value of the index.
Underlying Price in Black-Scholes Formulas
Call option premium under the Black-Scholes model is calculated using the following formula:
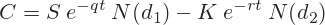
It may look complicated at first, but you can focus only on the letters C, S0, and X. These are the three prices explained above: C denotes call option premium, S0 denotes underlying price (the zero means it is now, at time zero), and X is the strike price (sometimes the letter K is used for strike instead of X).
If you ignore the other symbols in the formula, you can see that a call option price generally depends on the difference between underlying price and strike price (with some adjustments, which depend on the other inputs, such as volatility and time to expiration). In general, the more underlying price S0 exceeds strike price X, the more valuable a call option is.
Similarly, a put option price formula is:
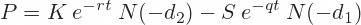
It is quite like the call option formula, only the order of S0 and X is reversed. The more strike price X exceeds underlying price S0, the more valuable a put option is (with some adjustments based on the other inputs).
Detailed explanation of the formulas including all the other symbols is available here.
Effect of Underlying Price on Call Option Price
The effect of underlying price on option prices is easiest to understand when visualized on a chart. In the Black-Scholes Calculator screenshot below you can see a two charts. Let's first focus on the green, upper chart.
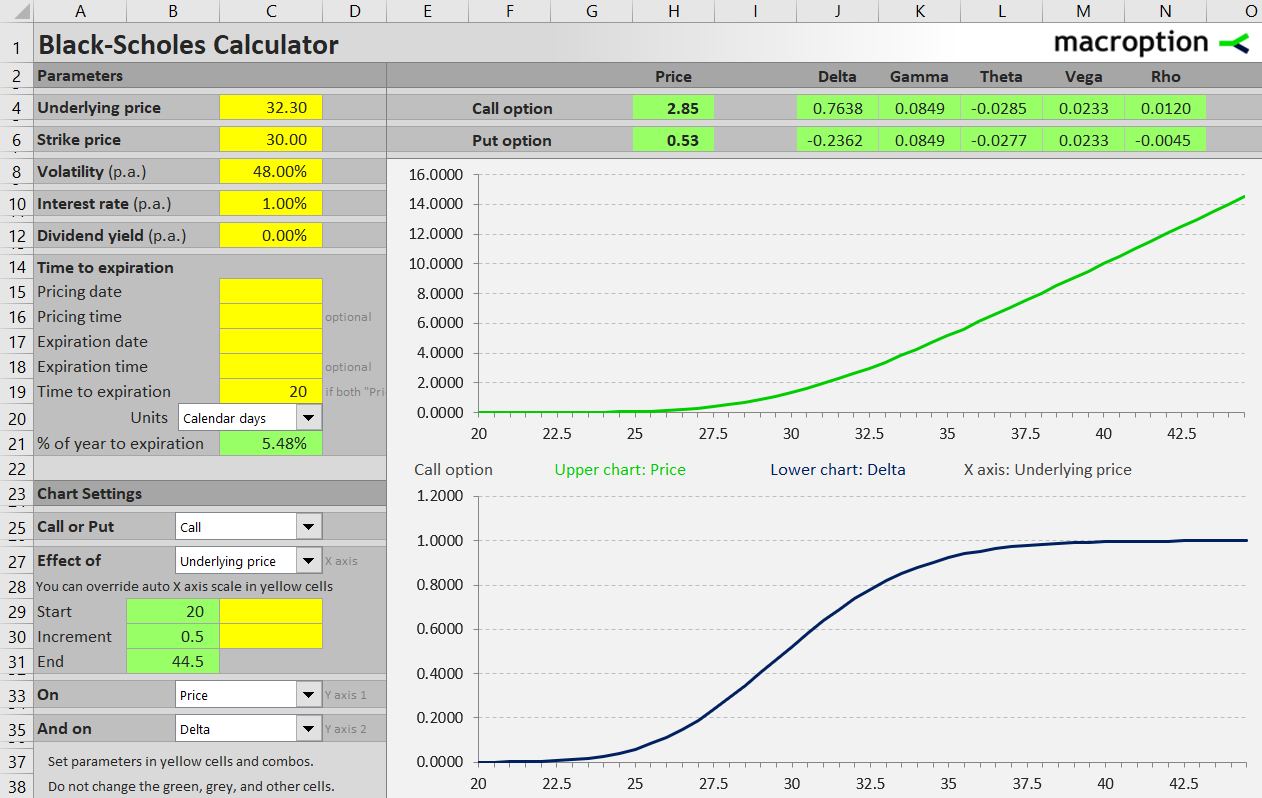
It shows the effect of underlying price (X-axis) in option premium (Y-axis). It is a call option with $30 strike price and 20 days remaining to expiration. Implied volatility is 48% (you can see all the inputs in the yellow cells in upper left corner).
The option premium if growing as underlying price increases. Initially, when underlying price is very low (the left end of the chart), the option premium is close to zero and not really growing much. The option is out of the money, which means you wouldn't benefit from exercising it, because you would effectively buy the underlying stock for the strike price $30, while you could buy it for a lower price in the stock market.
The graph starts to pick up once underlying price approaches the strike price ($30). Further up above the strike (when the option is in the money) it becomes almost a straight, upward sloping line, and option premium is growing in 1:1 linear proportion to underlying price.
Effect of Underlying Price on Put Option Price
With put options the effect of underlying price is inverse. The lower the underlying price, the higher the put option premium.
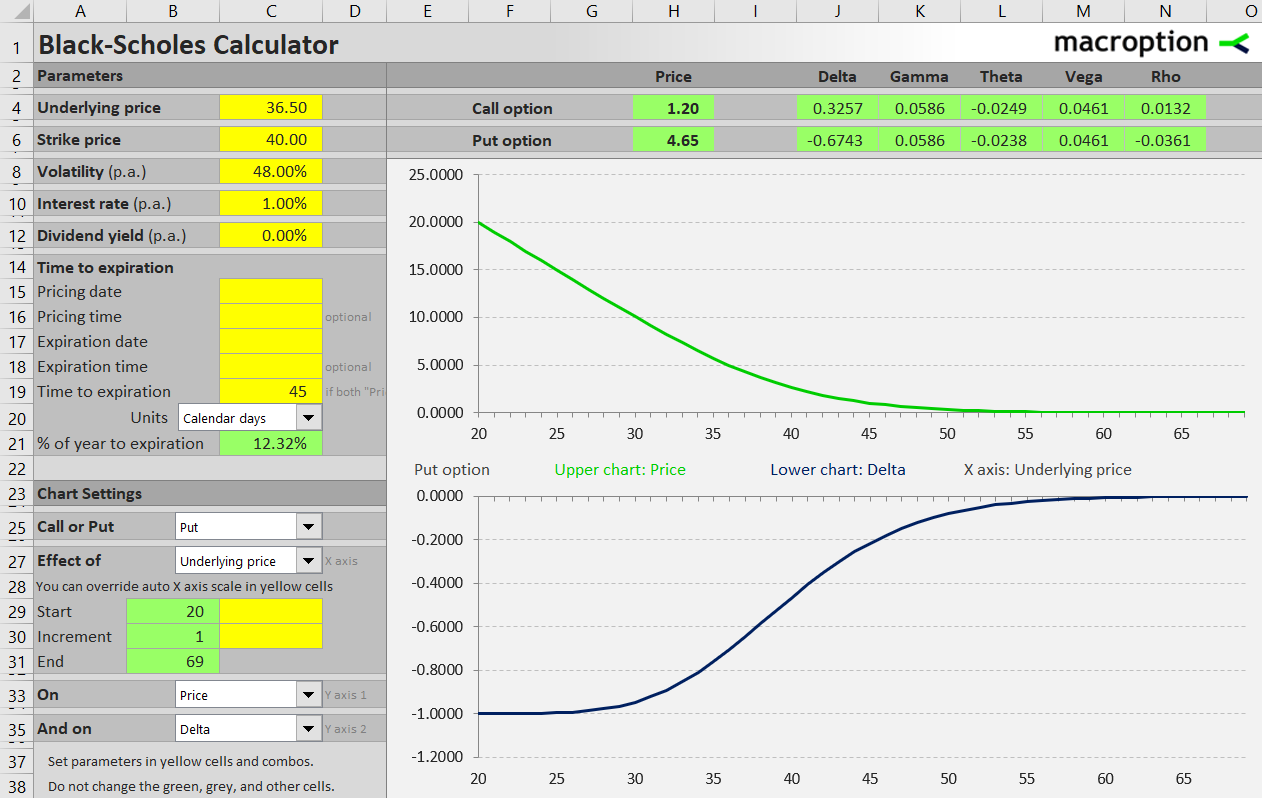
Option Delta
The lower blue chart in both screenshots is showing the option's delta as it changes with underlying price. Delta, one of option Greeks, provides a way to exactly measure the immediate effect of underlying price changes on option premium. The number shows by how many dollars option premium will change if underlying price increases by one dollar.
For call options, delta can reach values from 0 (option premium doesn't really increase at all – when option is out of the money, on the left end of the call chart) to +1 (option premium rises 1:1 with underlying price – deep in the money, right end of call chart).
For put options delta can reach the values from -1 (deep in the money for low underlying prices) to 0 (out of the money for high underlying prices).
You can see the exact delta value calculated in cells J4 (call) and J6 (put) in the screenshots.

For detailed instructions for working with underlying price in the calculator and modeling its effect on option prices and Greeks, see Working with Underlying Price in the Black-Scholes Calculator.
For overview of all the calculator's features and more screenshots, see Black-Scholes Calculator.