Sharpe Ratio Formula
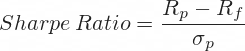
... where:
Rp = expected return of the portfolio or investment
Rf = risk-free interest rate
σp = standard deviation of portfolio returns
Here you can see detailed explanation of the formula.
Sharpe Ratio Value Range
Sharpe ratio can theoretically reach any value – positive, negative, or zero.
Here you can find more detailed explanation: Sharpe Ratio Range.
Here you can find the interpretation of negative Sharpe ratio.
Sharpe Ratio Papers and Resources
The following papers discuss the Sharpe ratio and its practical applications.
Sharpe ratio was originally invented by William F. Sharpe in 1966 and introduced in this paper:
William F. Sharpe: Mutual Fund Performance; first published in The Journal of Business, January 1966. Freely available as pdf download on Stanford University website:
www.stanford.edu/~wfsharpe/art/mfp.pdf
In 1994 Sharpe published a substantial revision of the Sharpe ratio:
William F. Sharpe: The Sharpe Ratio; first published in The Journal of Portfolio Management, Fall 1994. Freely available online on Stanford University website:
www.stanford.edu/~wfsharpe/art/sr/sr.htm
Papers covering practical applications and modifications of Sharpe ratio:
William F. Sharpe: Morningstar's Risk-adjusted Ratings; Stanford University, January 1998:
www.stanford.edu/~wfsharpe/art/msrar/msrar.htm
William F. Sharpe: Morningstar's Performance Measures; Stanford University:
www.stanford.edu/~wfsharpe/art/stars/stars0.htm
The Sharpe ratio part: www.stanford.edu/~wfsharpe/art/stars/stars6.htm
William F. Sharpe
William Forsyth Sharpe is STANCO 25 Professor of Finance, Emeritus, at Graduate School of Business, Stanford University, and 1990 Nobel Prize laureate. Most people associate him with the Sharpe ratio, but he has substantially contributed to numerous other key financial concepts, including the Capital Asset Pricing Model or binomial option pricing models.
The following resources are among the best if you want to quickly learn more about Professor Sharpe and his works:
Personal page of William F. Sharpe on Stanford University website. This page contains links to various papers, lecture videos and audios, and other resources by Professor Sharpe:
Detailed bio with all positions, awards, publications, and courses:
www.stanford.edu/~wfsharpe//bio/vitae.htm
William F. Sharpe page on Wikipedia:
en.wikipedia.org/wiki/William_Forsyth_Sharpe
William F. Sharpe autobiography on The Nobel Foundation website. It was written at the time of the Nobel Prize (1990), therefore it does not cover the later years:
www.nobelprize.org/nobel_prizes/economics/laureates/1990/sharpe-autobio.html