Why Is Volatility Proportional to the Square Root of Time?

Annualizing Volatility

When you want to annualize or de-annualize volatility (or transform volatility to any other time period), you need to multiply it by the square root of the time ratio, rather than the time ratio itself. For example, if you have monthly volatility and want to transform it to annual volatility, you multiply it by the square root of 12 and not by 12 directly.

Why Is Volatility Proportional to the Square Root of Time?

You can find the explanation in the calculation of volatility or in what volatility represents mathematically.

As most people in finance understand it, volatility is standard deviation of returns. The calculation of (historical) volatility goes like this:

1. Get daily closing prices of the security.
2. Calculate logarithmic returns for each day.
3. Calculate standard deviation of these logarithmic returns over a period of last N days.
4. The result (the standard deviation) is daily historical volatility.
5. If you want to transform it to annual volatility, multiply it by the square root of the number of trading days per year.

Standard deviation is the square root of variance, or the square root of the average squared deviation from the mean (see Calculating Variance and Standard Deviation in 4 Easy Steps).

Now finally why volatility is proportional to the square root of time rather than time directly:

The reason is in the assumption that common option pricing and volatility models take – the assumption that prices make the so called random walk, mathematically Wiener Process, but popularly better known as Brownian Motion (from physics).

You don't need to delve into the details of high mathematics (if you want, see Wikipedia), but the important thing to remember is that each particular increment of this random walk has variance that is proportional to the time over which the price was moving. For example, if a particular randomly walking stock has variance equal to 1 in 1 day, it has variance equal to 2 in 2 days etc.

Volatility, or standard deviation, is the square root of variance.

In mathematics the square root of a product of two numbers is equal to the product of their square roots:

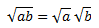
Now replace a with variance (denoted σ²) and b with time (denoted t). Volatility (denoted σ) is standard deviation of returns, which is the square root of variance:

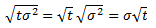
Summary

• For price making a random walk, variance is proportional to time.
• Standard deviation is the square root of variance and therefore it is proportional to the square root of time.
• Volatility is standard deviation and therefore it is proportional to the square root of time.