Which Values Can Sharpe Ratio Reach?
Sharpe ratio can theoretically reach any value.
It can be any number from negative infinite to positive infinite.
It is very obvious when you look at the Sharpe ratio formula:
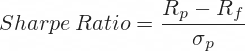
Sharpe ratio is portfolio excess return divided by standard deviation (or volatility) of portfolio returns. To understand the range of possible values of Sharpe ratio you need to understand the possible value ranges of its numerator (excess return) and denominator (volatility).
Excess Return Value Range
Excess return is the (expected or realized) return on the portfolio (or investment, fund, or trading strategy) less the risk-free return (typically treasury yield or money market interest rate). It can reach any value.
- It is positive when the investment's return is greater than the risk-free rate.
- It is negative when the investment's return is lower than the risk free rate.
- It is exactly zero when the investment's return is exactly equal to the risk-free rate.
Volatility Value Range
Volatility, or standard deviation of the investment's returns, can theoretically reach any positive value or it can be zero (it is zero when the returns are the same all the time). Volatility can not be negative.
Sharpe Ratio Value Range
From the ranges of possible values of excess return (numerator) and volatility (denominator), you can see that Sharpe ratio can theoretically reach any value.
Most of the time when people calculate and use Sharpe ratio, it is positive (otherwise there is not much sense in spending time to calculate it). Sharpe ratio is positive when excess return is positive, which is when the investment return is greater than the risk-free rate.
Sharpe ratio can also be zero. This is when the investment's excess return is zero, which is when the return on the portfolio is exactly equal to the risk-free rate.
Sharpe ratio can also be negative. Because the denominator (volatility) can never be negative, Sharpe ratio is negative when the numerator (excess return) is negative, which is when the return on the investment is smaller than the risk-free rate. See more detailed explanation of negative Sharpe ratio interpretation.
On both the positive and negative side, Sharpe ratio can theoretically be infinitely small (close to zero) and it can also be infinitely large (close to positive infinite or negative infinite). Excess return is usually not an extreme number (in the millions or greater), therefore it mainly depends on the standard deviation (volatility). When volatility is high, Sharpe ratio is smaller in absolute terms (for the same excess return). Conversely, when volatility is small, Sharpe ratio is a greater positive or negative number.
An extreme case would be when the volatility would equal zero. Mathematically you would not be able to calculate Sharpe ratio (dividing by zero). You could say that the ratio is close to infinite (positive or negative). However, there is no sense in calculating and interpreting Sharpe ratio when volatility is zero, because in that case the investment itself becomes risk-free (as investing theory understands it).