This page explains the Excel function SKEW, which calculates sample skewness, and how to convert its result to get population skewness.
Skew Excel Function
In Excel, skewness can be comfortably calculated using the SKEW Excel function. The only argument needed for SKEW function is the range of cells containing the data.
For example the formula:
=SKEW(B3:B102)... calculates skewness for the set of values contained in cells B3 through B102.
Calculating Sample Skewness in Excel
The built-in SKEW Excel function calculates sample skewness:
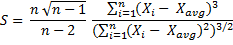
Here you can see a detailed derivation and explanation of skewness formula.
Calculating Population Skewness in Excel
Unlike with variance or standard deviation (which you can calculate for either sample or population in Excel), there is no direct built-in Excel function for population skewness. You can either calculate is directly...
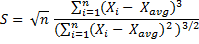
... or by adjusting the SKEW Excel function (this option usually leads to smaller Excel file size and better performance, as you don't need to calculate the individual deviations from the mean in extra cells).
Adjusting from Sample to Population Skewness in Excel
=SKEW(Data!$B$16:$B$10015)/SQRT($G$5*($G$5-1))*($G$5-2)This is the function I use in the Descriptive Statistics Calculator. The first part – SKEW(Data!$B$16:$B$10015) – is the built-in Excel SKEW function for sample skewness of cells B16 through B10015, and the rest is the adjustment from sample to population skewness, where cell G5 calculates population size:
=COUNT(Data!$B$16:$B$10015)The whole formula is:
Population Skewness = Sample Skewness · (n – 2) / Square root of (n (n – 1))
... where n = population size (number of values)
You can see how skewness Excel calculation works in practice in the Descriptive Statistics Calculator.