This page explains the formula for population and sample skewness. You can easily calculate skewness in Excel using the Descriptive Statistics Calculator.
If you don't want to go through the lengthy derivation and explanation below, the formulas are here:
Population Skewness Formula:
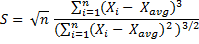
Sample Skewness Formula:
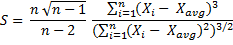
Detailed derivation and explanation of the formulas follows.
What Is Skewness?
Skewness is one of the summary statistics. It is used for describing or estimating symmetry of a distribution (relative frequency of positive and negative extreme values).
In finance, it is used in portfolio management, risk management, option pricing, and trading.
Skewness Definition
Skewness is the ratio of (1) the third moment and (2) the second moment raised to the power of 3/2 (= the ratio of the third moment and standard deviation cubed):
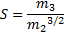
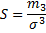
Deviations from the Mean
For calculating skewness, you first need to calculate each observation's deviation from the mean (the difference between each value and arithmetic average of all values). The deviation from the mean for ith observation equals:
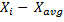
Third Moment Formula
The third moment about the mean is the sum of each value's deviation from the mean cubed, which (the whole sum) is then divided by the number of values:
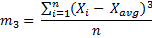
Second Moment Formula
The second moment about the mean is the sum of each value's squared deviation from the mean, divided by the number of values. This is the same formula as the one you probably know as variance (σ2). Variance is standard deviation (σ) squared.
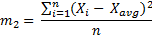
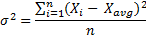
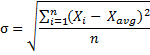
Population Skewness Formula
The direct skewness formula (ratio of the third moment and standard deviation cubed) therefore is:
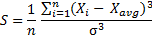
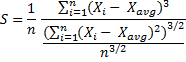
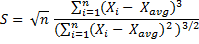
Sample Skewness Formula
The formulas above are for population skewness (when your data set includes the entire population). Very often, you don't have data for the whole population and you need to estimate population skewness from a sample.
When calculating sample skewness, you need to make a small adjustment to the skewness formula (the function of the adjustment is to correct a bias inherent in small samples):
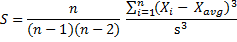
... where:
- n = sample size
- s = sample standard deviation:
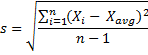
Therefore:
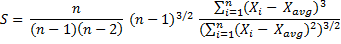
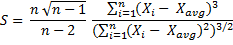
For a very large sample (very high n), the differences between and among n, n-1, and n-2 are becoming negligible, and the sample skewness formula approximately equals:
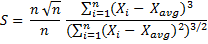
And therefore approximately equals population skewness formula:
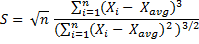
You can easily calculate skewness, kurtosis, and other measures in Excel using the Descriptive Statistics Excel Calculator.