This page explains the time to expiration input in the Black-Scholes option pricing model. We will discuss which time units to use, how to work with fractions of days, how time enters the formulas, and how it affects the resulting option prices.
Time to Expiration in the Black-Scholes Model
Options have limited life and the time remaining to expiration is one of the key factors affecting their prices. Most people are familiar with the concept of time value and time decay – option prices typically decrease with passing time, other things being equal. The Black-Scholes model can quantify this process and exactly measure an option's sensitivity to passing time (mainly in the form of theta).
Time to expiration is one of the five/six inputs of the Black-Scholes model (the others are underlying price, strike price, volatility, interest rate, and – under Merton's dividend extension – dividend yield).
Which Time Units to Use
Time can be measured in different units – days, weeks, hours, minutes, seconds... Which units should be used when working with time in the Black-Scholes model?
The common approach is to enter time to expiration in years.
For example, an option expiring in 3 months with have the time to expiration input entered as 0.25 or 25%.
Theoretically, it is not absolutely necessary to work with time in years – you could possibly enter it as number of months, days, or seconds – but in any case the units of time must match units of the other inputs, namely volatility, interest rate, and dividend yield. These are typically presented in annualized form, which corresponds to time entered in years.
How exactly do we calculate time to expiration in years to enter in a Black-Scholes pricing formula?
In practice, option traders typically work with days remaining to expiration. To convert these to percentage of year, divide the number of days to expiration by the number of days per year.
For example, for an option that expires in 30 days, the Black-Scholes time to expiration input is 30/365 = 0.0822 or 8.22%.
Fractions of Days
Fractions of days are often used for more precision. This is recommended particularly for short-dated options.
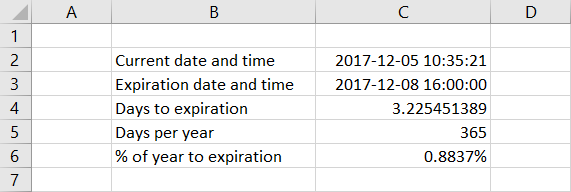
For example, when pricing an option that expires at 4 pm on Friday and the current day and time is Tuesday 10:35:21 am, you can calculate the time input as follows:
The time left to expiration is 3 days, 5 hours, 24 minutes, and 39 seconds. Converting it to fractional days, we get 3.225451, which we then divide by the number of days per year. The resulting time to expiration as percentage of year is 0.8837%.
This is easy to do in Excel, where you can simply subtract the current date and time from the expiration date and time.
Calendar Days or Trading Days?
Although calendar days are more commonly used, some option traders prefer to work with trading days, which can be justified by the fact that events possibly causing a move in underlying price are far less likely on weekends or holidays (on the other hand, interest, which is another Black-Scholes input, accrues based on calendar days).
If you choose to work with trading days, make sure to divide them by the number of trading days per year (not calendar days) to get the correct time input. For example, if the option has 21 trading days remaining to expiration, the Black-Scholes time input is 21/252 = 0.0833 or 8.33%, assuming 252 trading days in a year, which has been the average for US traded options in the recent years.
Notation
When presenting the Black-Scholes formulas, different sources use different symbols for the inputs. Time to expiration is most commonly denoted by lower or upper case t or T.
Alternatively, some sources use T – t, where T denotes expiration time, t is the current time (at the moment of pricing the option), and the difference is the length of period between now and expiration. The original Black and Scholes paper uses a similar notation t* – t, where t* denotes expiration time and t is the time of pricing.
Throughout the Macroption website and in all the calculators' user guides I use lower case t for time to expiration as % of year, unless stated otherwise. I use capital T for number of days to expiration (not divided by days per year).
Time in Option Price Formulas
Time to expiration enters the call and put option price formulas in several ways. It amplifies the effects of volatility, interest rate, and dividend yield.
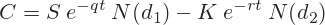
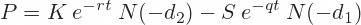
Interest rate and dividend yield are always multiplied by time to expiration when entering the formulas. This makes sense, as the effects of interest and dividend yield compound with time.
The expression
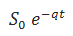
is the current underlying price S0 adjusted for dividend income (using continuously compounded dividend yield q).
The expression
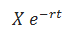
is present value of the option's strike price X (using continuously compounded risk-free interest rate r).
In the formulas for d1 and d2, volatility σ is multiplied by the square root of time.
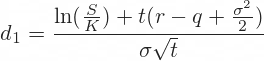
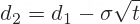
Like interest, the effect of volatility grows with time, but volatility is proportional to square root of time, not to time itself. For instance, you can expect a stock to move more in a year than in a month, but not 12x more, as some of the monthly moves offset each other.
Effect of Time on Option Prices
Most options lose value with passing time – this process is known as time decay.
The speed of time decay, measured by the option Greek theta, depends on a number of factors – generally on all the Black-Scholes inputs, including time to expiration itself – the rate of time decay is not constant in time.
The time when an option loses the most of its time value depends mainly on the option's moneyness. At the money options tend to lose most time value in the final days (and hours) before expiration. In the money and out of the money options, which have less time value to start with, tend to lose it earlier. Far out of the money options often become virtually worthless even when many days still remain to expiration, because their strikes are so far from the current underlying price that their chance of getting in the money before expiration is almost zero.
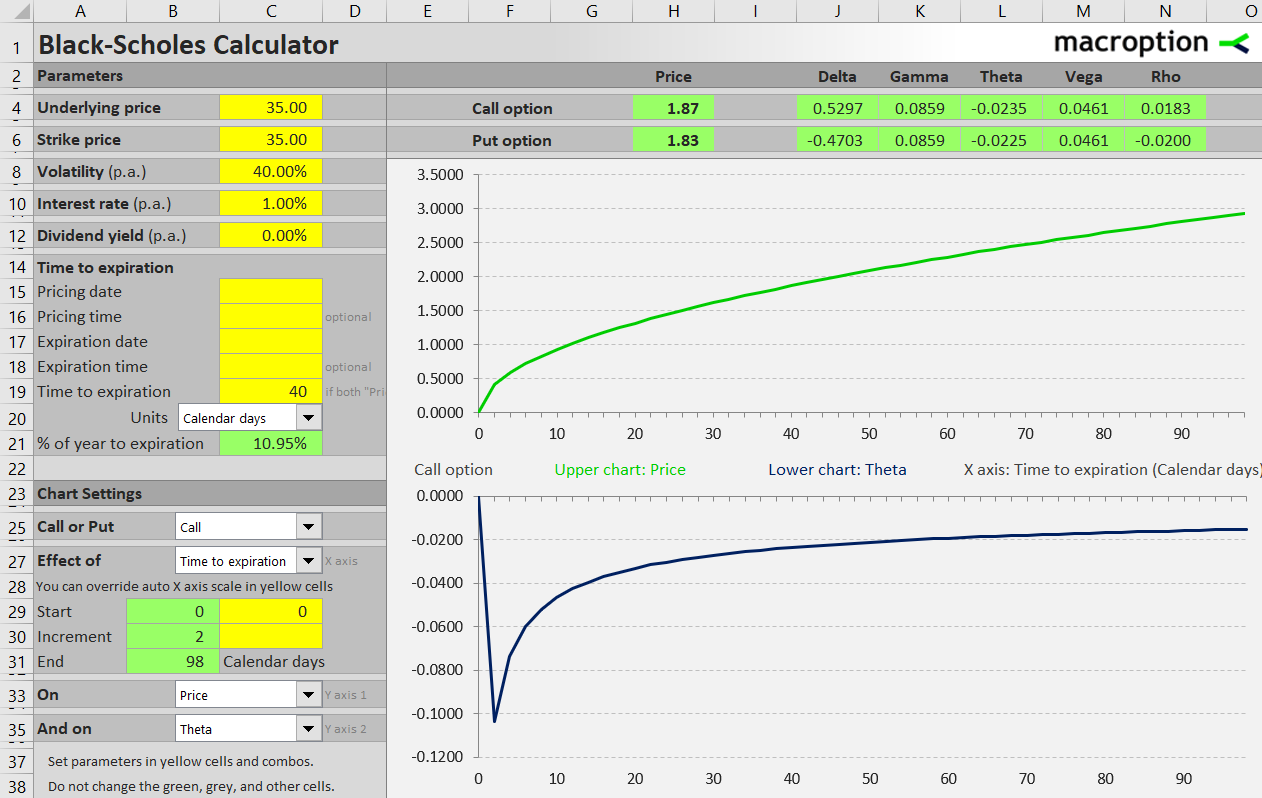
The example below shows how the price (upper green chart) and theta (lower blue chart) of an at the money call option ($35 strike, $35 underlying price) depend on time to expiration (X-axis). Time decay accelerates in the final days. Theta, which shows how much the option's price will change in the next day (other things being constant) is most negative just before expiration, before dropping to zero as the option expires.
Another example below shows an out of the money call option (strike $45). Its price drops below 5 cents and theta to almost zero more than a month before expiration. Notice the difference in curve shapes compared to the at the money example.
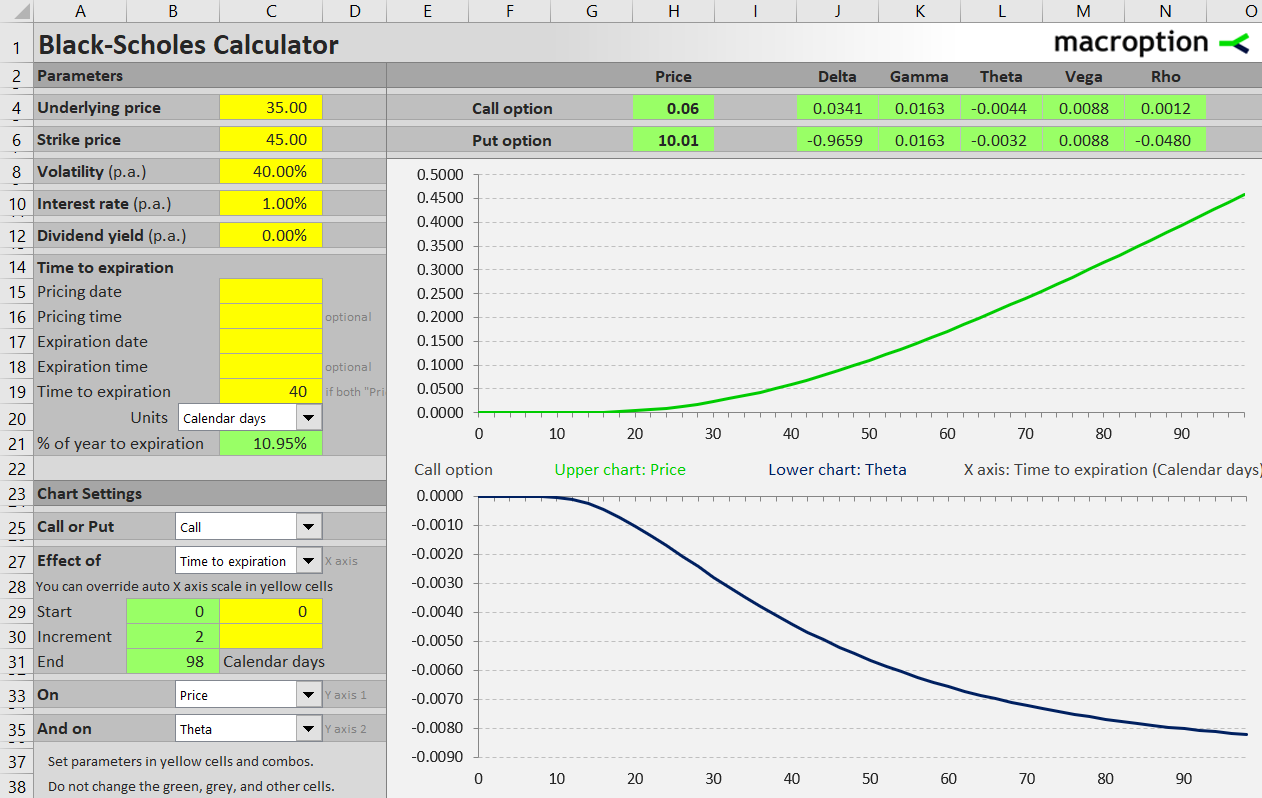
Time value and time decay also depend on volatility: the higher implied volatility, the greater time value and faster time decay. Typically to a much smaller extent, they also depend on interest rate and dividend yield.
Some combinations of these factors may lead to unusual time decay patterns. For instance, in the money calls on high dividend stocks or in the money puts can actually have negative time value and positive theta in the last days before expiration. The below example shows an in the money put in a high interest environment, where the effect can be strong enough to be noticeable.
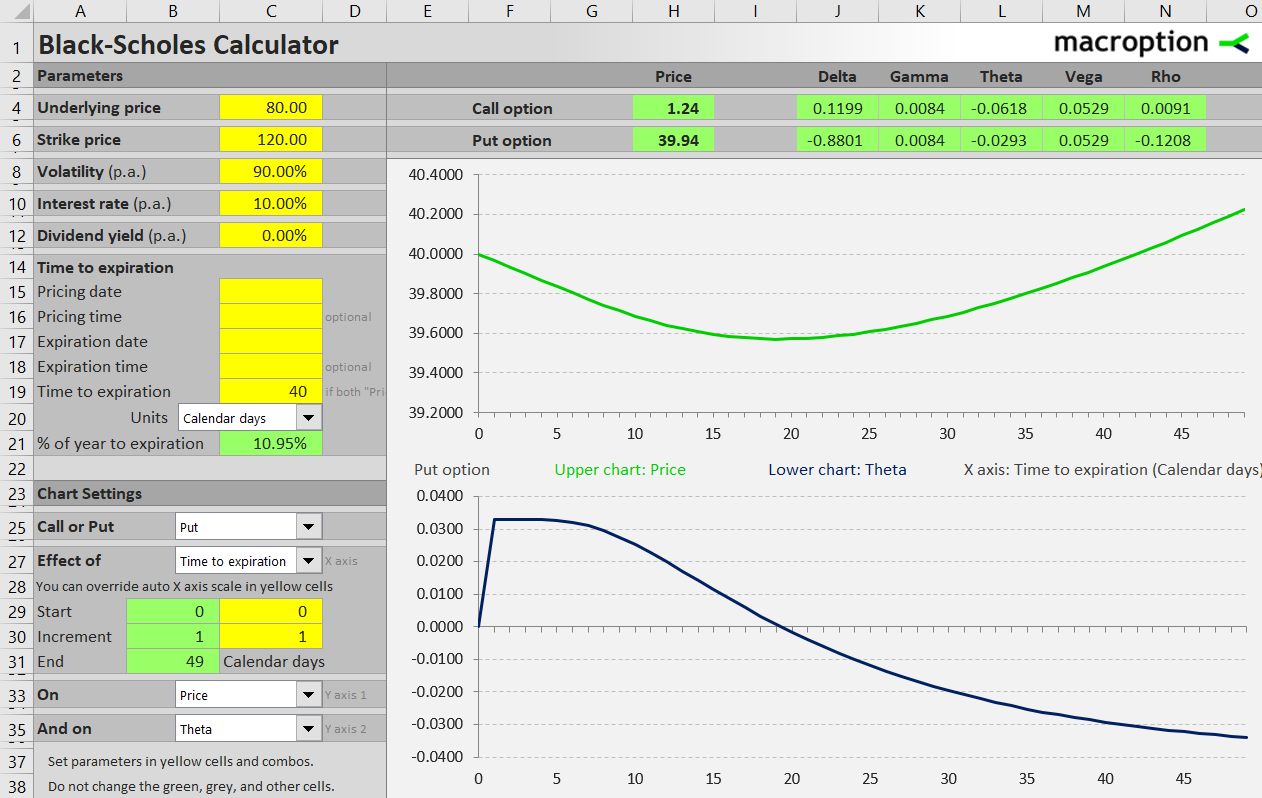
Detailed instructions for modeling effects of time to expiration on option prices and Greeks in the Black-Scholes Calculator are available here:
Working with Time to Expiration in the Black-Scholes Calculator