This page explains the Black-Scholes formulas for d1, d2, call option price, put option price, and formulas for the most common option Greeks (delta, gamma, theta, vega, and rho).
Black-Scholes Inputs
According to the Black-Scholes option pricing model (its Merton's extension that accounts for dividends), there are six parameters which affect option prices:
S = underlying price ($$$ per share)
K = strike price ($$$ per share)
σ = volatility (% p.a.)
r = continuously compounded risk-free interest rate (% p.a.)
q = continuously compounded dividend yield (% p.a.)
t = time to expiration (% of year)
In many sources you can find different symbols for some of these parameters. For example, strike price (here K) is often denoted X, underlying price (here S) is often denoted S0, and time to expiration (here t) is often denoted T – t (as difference between expiration and now).
In the original Black and Scholes paper (The Pricing of Options and Corporate Liabilities, 1973) the parameters were denoted x (underlying price), c (strike price), v (volatility), r (interest rate), and t* – t (time to expiration). Dividend yield was only added by Merton in Theory of Rational Option Pricing, 1973.
Call and Put Option Price Formulas
Call option (C) and put option (P) prices are calculated using the following formulas:
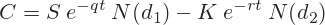
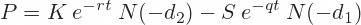
N(x) is the standard normal cumulative distribution function:
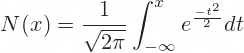
d1 and d2
The formulas for d1 and d2 are:
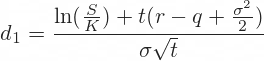
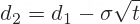
Original Black-Scholes vs. Merton's Formulas
In the original Black-Scholes model, which doesn't account for dividends, the equations are the same as above except:
- There is just S in place of Se-qt
- There is no q in the formula for d1
Therefore, if dividend yield is zero, then e-qt = 1 and the models are identical.
Black-Scholes Greeks Formulas
Below you can find formulas for the most commonly used option Greeks. Some of the Greeks (gamma and vega) are the same for calls and puts. Other Greeks (delta, theta, and rho) are different. Differences between the Greek formulas for calls and puts are often very small – usually a minus sign here and there. It is very easy to make a mistake.
Besides the already familiar N(d1), some of the Greek formulas (namely gamma, theta, and vega) use the term N'(d1) – with an apostrophe after N, indicating a derivative. This is the standard normal probability density function:
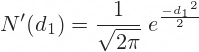
Delta
Delta is the first derivative of option price with respect to underlying price S. The formulas for call and put option delta are the following:
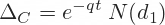
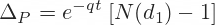
Sometimes you can see the put delta formula written as:
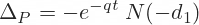
Notice the extra minus sign before e and another before d1.
This formula is identical to the first one. Because the standard normal distribution is symmetric and centered at zero, the standard normal cumulative distribution function has a very useful property:
N(–x) = 1 – N(x)
– N(–x) = N(x) – 1
– N(–d1) = N(d1) – 1
Relationship between Call and Put Delta
It is often said that (the absolute values of) call delta and put delta add up to 1.
If call delta is +1 (deep in the money), put delta is 0 (far out of the money). If call delta is 0, put delta is –1. If call delta is +0.7, put delta is –0.3.
The actual relationship is:
ΔC – ΔP = 1
However, this only holds without dividends.
If dividend yield q is zero, then e-qt is 1. Then call delta is N(d1) and put delta is N(d1) – 1.
With nonzero dividend yield, e-qt is slightly smaller than 1 and the above relationship does not hold exactly (usually it is still very close to 1, unless the yield q is very big and time to expiration t very long).
Gamma
Gamma is the second derivative of option price with respect to underlying price S. It is the same for calls and puts.
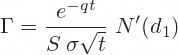
Theta
Theta is the first derivative of option price with respect to time to expiration t.
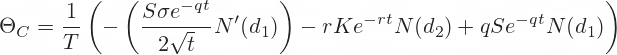
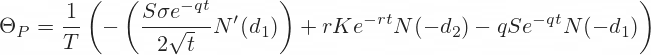
T is the number of days per year.
If T is calendar days (365), then the resulting theta is change in option price per one calendar day (or 1/365 of a year).
If T is trading days (about 252), theta is change in option price per one trading day (or 1/252 of a year).
Without the initial 1/T term, theta would be change per one year, which would be a period too long to be useful for most options.
Furthermore, different sources present the theta formulas with different signs (before the main terms).
The format used on this page calculates theta as change in option price if time to expiration decreases by one day. Therefore, negative theta means the option will lose value as time passes, which is the case with most (though not all) options.
For example, if an option's price is $2.50 today and theta is -0.50, we can expect the option to be worth $2.00 tomorrow.
If we used the alternative formula with opposite signs before the three main terms, theta would be +0.50 in this case. It would still mean the same thing, just expressed differently: Option price increases by $0.50 if time to expiration increases by one day (we would be going backwards in time).
The format used on this page appears to be the more popular one, although the other is still quite common.
Vega
Vega is the first derivative of option price with respect to volatility σ. It is the same for calls and puts.
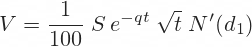
Note: Divide by 100 to get the resulting vega as option price change for one percentage point change in volatility (if you don't, it is for 100 percentage points change in volatility; same logic applies to rho below).
Rho
Rho is the first derivative of option price with respect to interest rate r. It is different for calls and puts.


Call options are generally more valuable when interest rates are high (because a call option can be considered an alternative to owning the underlying, or a way of funding). Conversely, put options are generally more valuable when interest rates are low.
That said, if the underlying pays dividends, it is mainly the interest rate net of dividend yield (r – q) rather than interest rate itself (r) that drives option prices.
Black-Scholes Formulas in Excel
All these formulas for option prices and Greeks are relatively easy to implement in Excel (the most advanced functions you will need are NORM.DIST, EXP and LN). You can continue to the Black-Scholes Excel Tutorial, where I have demonstrated the Excel calculations step-by-step (first part is for option prices, second part for Greeks).
Or you can get a ready-made Black-Scholes Excel Calculator.