Holding VIX futures and options past the close of the last trading day and waiting for the final settlement value to determine your profit or loss is widely considered a gamble. It is impossible to predict how the VIX will change from close to next day open, let alone what the final settlement value will be (and I leave the speculations about if and how much it is manipulated to others).
But trading is about statistics and probabilities and there have already been more than a hundred VIX expirations. In this post, which originated as a follow-up to my earlier tweet, I look at historical statistics of the differences between VIX options and futures final settlement values and spot VIX index closing values on the last days before expiration.
If you need a little background, see VIX Options Expiration, VIX Special Opening Quotation (SOQ), and VIX Expiration Calendar.
Let's start with an overview of the last two years. For each VIX expiration you can see the spot VIX index close on Monday (the day before the last trading day), the spot VIX index close on Tuesday (the last trading day), and the final settlement value, as well as the changes from Monday to Tuesday and from Tuesday to final settlement value.
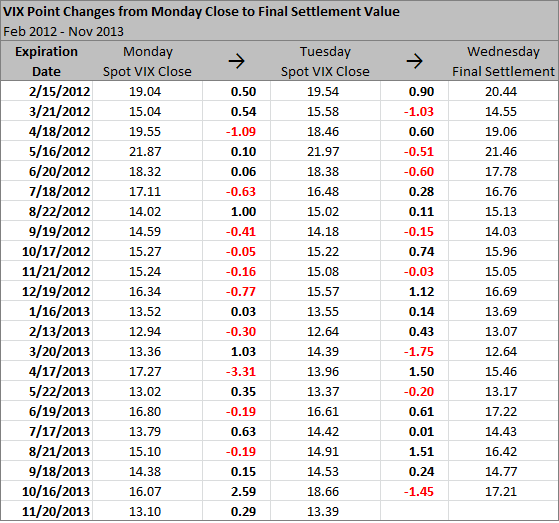
A few observations:
- Majority of changes (both Mon-Tue and Tue-Wed) have been quite small (roughly 3/4 changes smaller than 1 VIX point).
- The changes have been both positive and negative, with no apparent bias to either side (just by looking at the table).
- The most interesting observation: In 5 out of the last 11 VIX expirations the change from Tuesday VIX close to the final settlement value was greater than 1 VIX point.
Let's look at the whole history of VIX expirations and the summary statistics. I have only included VIX expirations when the final settlement was on Wednesday and the Monday and Tuesday before that were not holidays (as on some past January and February expirations).
There have been 100 such expirations so far (out of 110 total).
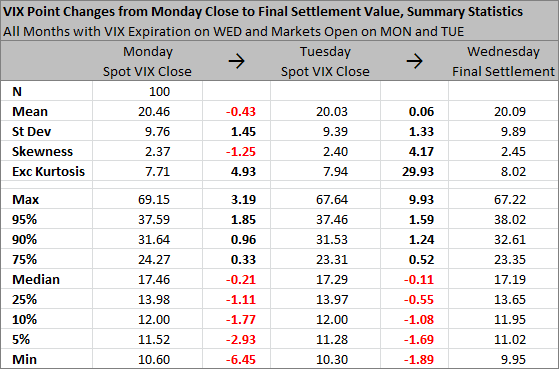
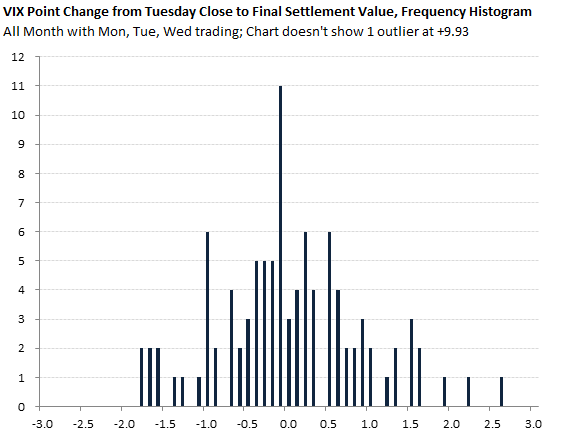
Let's focus mainly on the changes from Tuesday to the final settlement value, which are more interesting for this analysis. Mean and median are not far from zero. The changes are positively skewed and there is very high kurtosis (fat tails). However, most of it can be attributed to one outlier: +9.93 in October 2008 (change from 53 to 63). Without that month in the sample, the skewness and kurtosis would be +0.27 and +0.30, respectively, and the distribution would get quite close to normal.
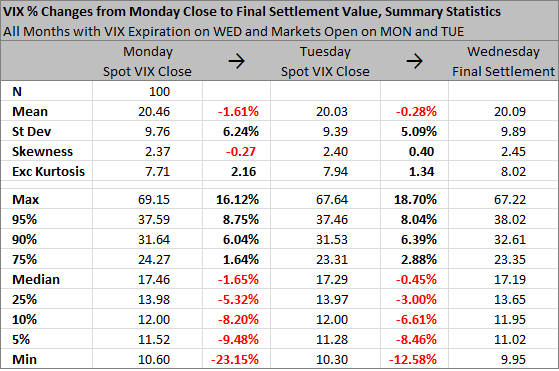
Which brings us to the idea that maybe we should work with percentage changes rather than VIX point changes. The table is below.
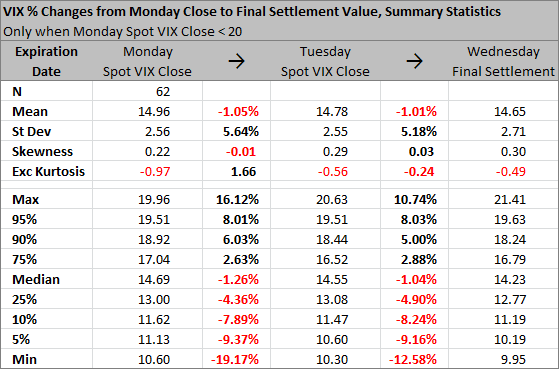
Alternatively, we can eliminate the periods of high VIX from the sample, as there are good reasons for expecting the VIX to behave differently in times of low volatility and in times of high volatility. If we only include the expirations when Monday spot VIX close was below 20, we are left with 62 observations which are perhaps more relevant to the current situation in the markets.
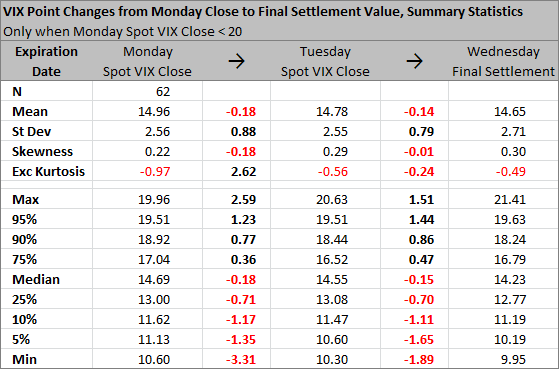
In low volatility times, the skewness and kurtosis are negative, but so small that the distribution can be considered normal. Mean is -0.14 and standard deviation is 0.79 VIX points. Also note the maximum (+1.51) and minimum (-1.89) – no far extremes here.
For the sake of completeness, below you can see the table for percentage changes in VIX<20 times. As expected, the findings are in line with the above.
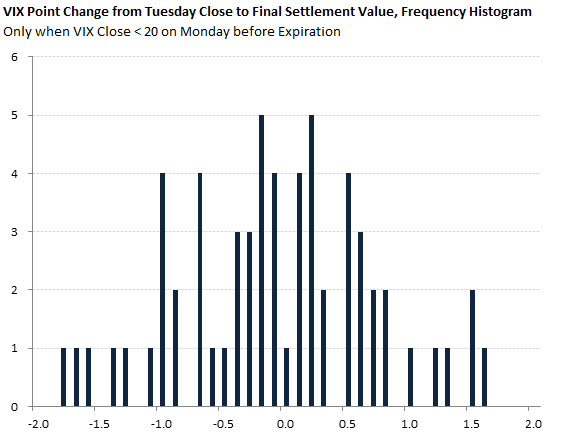
The most important observations for the low volatility sample are the following:
- Slightly negative mean/median. Final settlement value is slightly more likely to be lower than higher than Tuesday close.
- The distribution is almost normal.
- There haven't been any outliers much farther than 2 standard deviations from the mean (+2.08 and -2.21 sigma to be precise). This is best visible in the frequency histogram below.
For comparison, here is also the frequency histogram for the all VIX values sample. You can see that except the one huge outlier (not shown in the chart) it is only moderately positively skewed.
The last number, and maybe the most interesting number in the whole post, is the correlation between the Mon-Tue and Tue-Wed point changes. It is -0.01 for all the 100 expirations, but -0.30 for the 62 expirations when VIX closed below 20 on Monday. In other words, in periods of low volatility, when VIX has risen on Tuesday, the final settlement value is slightly more likely to be lower than Tuesday VIX close. But of course, a correlation of -0.30 on a sample of 62 is not a good basis for strong conclusions (furthermore, if we remove April 2013 from the sample, with the changes of -3.31 and +1.50, the correlation becomes -0.21).